Las matemáticas siempre han sido un reino de maravillas, donde la búsqueda de soluciones a problemas complejos ha intrigado y cautivado a los estudiosos durante siglos. En esta guía nos adentramos en el mundo de los problemas matemáticos más difíciles, explorando sus entresijos y la continua búsqueda de sus soluciones. Desde la enigmática conjetura de Goldbach hasta la escurridiza hipótesis de Riemann, cada problema presenta sus propios desafíos, inspirando a los matemáticos a superar los límites del conocimiento humano. Para aquellos que se encuentran fascinados pero perplejos ante estos complejos problemas, buscar la ayuda de los mejores servicios de tutoría en línea puede ser una forma excelente de profundizar en los problemas.

✅ Escritor de Ensayo de IA ✅ Detector de IA ✅ Detector de Plagio ✅ Parafraseador
✅ Resumidor ✅ Generador de Citaciones
La Conjetura de Goldbach
La Conjetura de Goldbach, formulada por Christian Goldbach en 1742, es un enigma matemático que gira en torno a la expresión de números pares como suma de dos números primos. La Conjetura de Goldbach se considera uno de los problemas matemáticos más difíciles. Por ejemplo, el número 10 puede expresarse como 7 + 3, donde 7 y 3 son números primos.
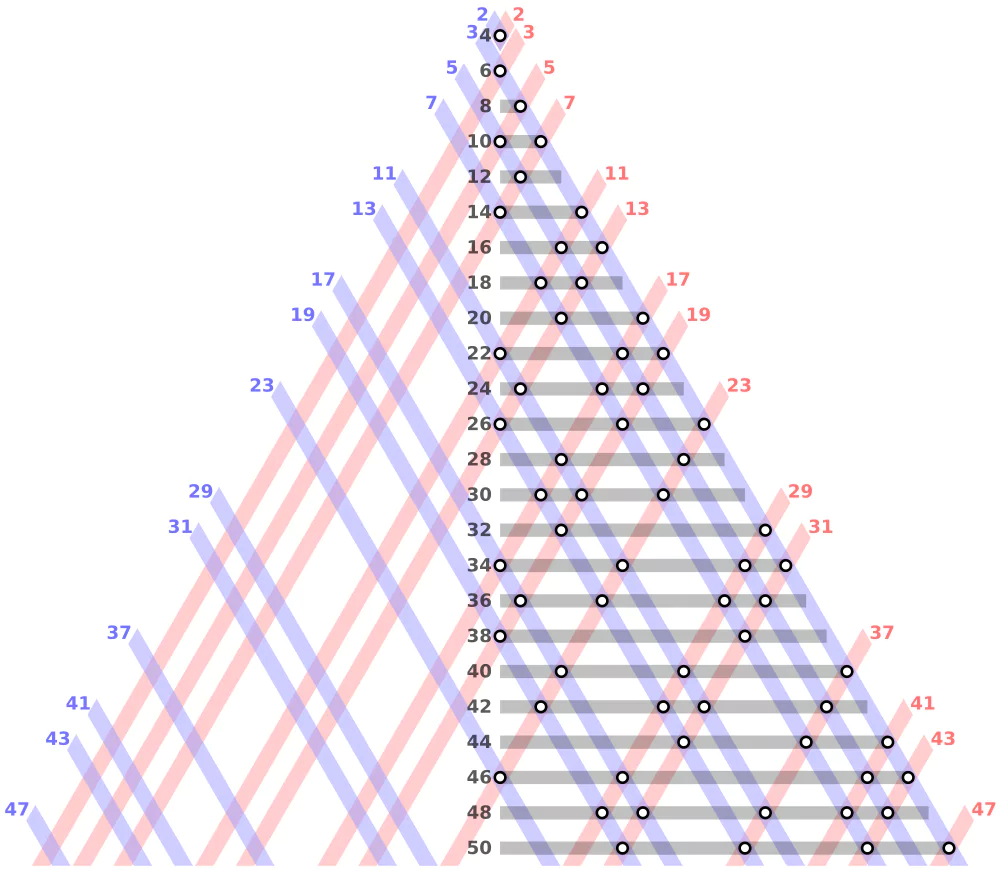
A pesar de los grandes esfuerzos realizados por los matemáticos, sigue sin encontrarse una demostración analítica de la conjetura de Goldbach. Aunque la conjetura se ha verificado para numerosos números enteros pares, aún no se ha descubierto una prueba rigurosa que se aplique a todos los casos. La distribución de los números primos proporciona una justificación informal de la conjetura, ya que es más probable que los números enteros más grandes se expresen como la suma de dos primos.
The Inscribed Square Problem
El problema del cuadrado inscrito plantea una pregunta fascinante: ¿Puede cualquier curva cerrada y no intersecante contener cuatro puntos que formen un cuadrado? Los matemáticos han explorado este problema en diversos contextos, examinando distintos tipos de curvas y su relación con los cuadrados inscribibles.
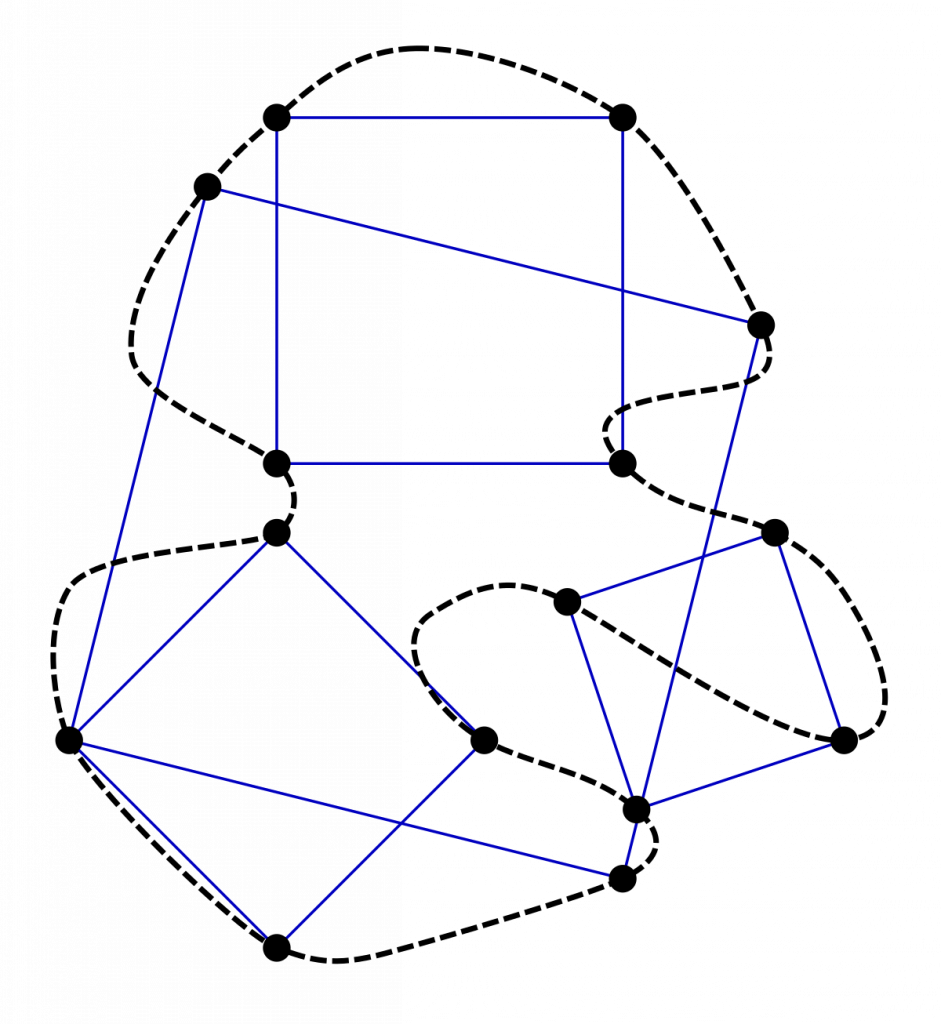
Aunque el caso general del problema de los cuadrados inscribibles sigue sin resolverse, se han demostrado casos concretos. Por ejemplo, se ha establecido que los círculos y los cuadrados tienen un número infinito de cuadrados inscribibles. Los triángulos obtusos tienen exactamente uno, mientras que los triángulos rectángulos y agudos tienen dos y tres cuadrados inscribibles, respectivamente.
La Hipótesis del Continuo
La Hipótesis del Continuo se adentra en el vasto reino de los infinitos. En matemáticas, existen diferentes magnitudes de infinito, dependiendo del tamaño y la naturaleza de los conjuntos implicados. Los infinitos contables, representados por conjuntos que pueden ponerse en correspondencia 1 a 1 con los números enteros positivos, son distintos de los infinitos incontables.
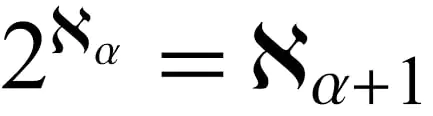
Los trabajos de Georg Cantor en el siglo XIX revelaron que el conjunto de los números reales es incontable, lo que significa que no puede emparejarse con los números enteros positivos de manera unívoca. La Hipótesis del Continuo plantea si existe un infinito que se sitúe entre los infinitos contables e incontables. Sin embargo, las técnicas matemáticas actuales no pueden resolver o refutar esta hipótesis, ya que requiere un nuevo marco para la teoría de conjuntos.
La Conjetura de Collatz
La conjetura de Collatz presenta un problema aparentemente sencillo pero de una complejidad intrigante. Se trata de construir una secuencia iterativa a partir de un número positivo. Si el número es par, se divide por 2; si es impar, se multiplica por 3 y se añade 1. La conjetura afirma que, independientemente del valor inicial, esta secuencia acabará alcanzando el número 1.
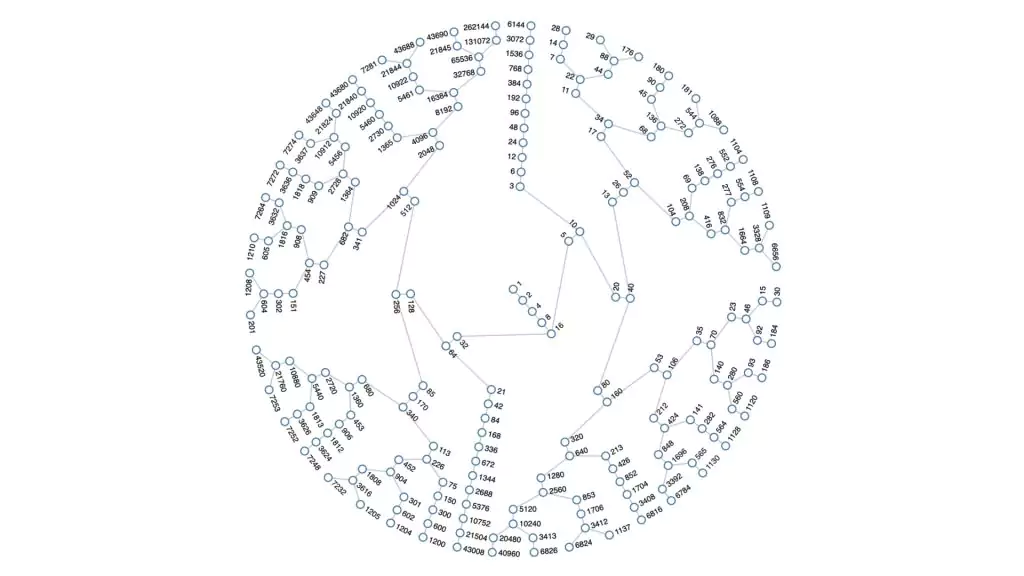
Explorar la conjetura de Collatz a través de ejemplos puede proporcionarnos una idea de su cautivadora naturaleza. Empezando con el número 12, tenemos la secuencia: 12, 6, 3, 10, 5, 16, 8, 4, 2, 1. Del mismo modo, a partir de 19, tenemos: 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. A pesar de la extensa exploración, no se ha encontrado ningún patrón o prueba que apoye o refute la conjetura.
Resolver el Ajedrez
Resolver el ajedrez implica encontrar una estrategia óptima que garantice la victoria en cada partida. Aunque se han descubierto estrategias óptimas para juegos más sencillos, como el conecta 4 o el tres en raya, la complejidad del ajedrez plantea un reto inmenso. El gran número de posibles variantes del juego hace que sea inviable desde el punto de vista computacional buscar exhaustivamente una jugada óptima.
Para hacer frente a la complejidad del ajedrez, los investigadores han desarrollado potentes sistemas de inteligencia artificial (IA). Estos sistemas de IA, como Deep Blue y AlphaZero, utilizan algoritmos avanzados y redes neuronales para analizar grandes cantidades de datos e identificar estrategias ganadoras. Sin embargo, es importante señalar que estos sistemas de IA no resuelven el ajedrez en el sentido tradicional, sino que se basan en una gran capacidad de cálculo y análisis de datos.
La Hipótesis de Riemann
La Hipótesis de Riemann, propuesta por Bernhard Riemann en 1859, tiene una inmensa importancia en el campo de la teoría de números. Se centra en la distribución de ceros no triviales de la función zeta de Riemann, una función matemática con importantes aplicaciones en diversas áreas de las matemáticas.
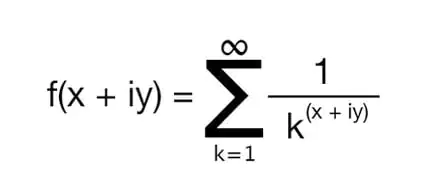
Las profundas implicaciones de la hipótesis de Riemann van más allá de la teoría de números, con conexiones con la distribución de números primos y el comportamiento de las funciones matemáticas. A pesar de su importancia fundamental, los matemáticos aún no han demostrado ni refutado la hipótesis. Su complejidad y la ausencia de una demostración definitiva le han valido el estatus de uno de los problemas sin resolver más desafiantes de las matemáticas.
Conclusión
Los problemas matemáticos más difíciles siguen cautivando a matemáticos de todo el mundo, ampliando los límites del conocimiento y la comprensión humanos. Desde la eterna búsqueda de la conjetura de Goldbach y las complejidades de los cuadrados inscritos hasta el enigma de la hipótesis de Riemann, estos problemas simbolizan la búsqueda incesante de la verdad y el encanto de lo desconocido. Mientras los matemáticos persisten en su exploración, los misterios de estos problemas siguen sin resolverse, alimentando la curiosidad e inspirando a las generaciones futuras para abordar los enigmas matemáticos más desafiantes.
FAQ
Síguenos en Reddit para más información y actualizaciones.




Comentarios (0)
¡Bienvenido a los comentarios de A*Help!
El debate y la discusión son lo nuestro en A*Help.
Valoramos la diversidad de opiniones de los usuarios, así que puede que encuentres puntos de vista con los que no estés de acuerdo. Y eso está bien. Sin embargo, hay ciertas cosas con las que no estamos de acuerdo: los intentos de manipular nuestros datos de cualquier manera, por ejemplo, o la publicación de material discriminatorio, ofensivo, odioso o despectivo.