What Is the Hardest Math Problem?

Mathematics has always been a realm of wonder, where the quest for solutions to complex problems has intrigued and captivated scholars for centuries. In this guide, we delve into the world of the hardest math problems, exploring their intricacies and the ongoing pursuit of their solutions. From the enigmatic Goldbach Conjecture to the elusive Riemann Hypothesis, each problem presents its unique challenges, inspiring mathematicians to push the boundaries of human understanding. For those who find themselves fascinated but perplexed by these complex problems, seeking help from the best online tutoring services can be an excellent way to dive deeper into the problems.

The Goldbach Conjecture

The Goldbach Conjecture, formulated by Christian Goldbach in 1742, is a mathematical puzzle that revolves around expressing even numbers as the sum of two prime numbers. The Goldbach Conjecture is considered to be one of the hardest math problems. For instance, the number 10 can be expressed as 7 + 3, where 7 and 3 are prime numbers.

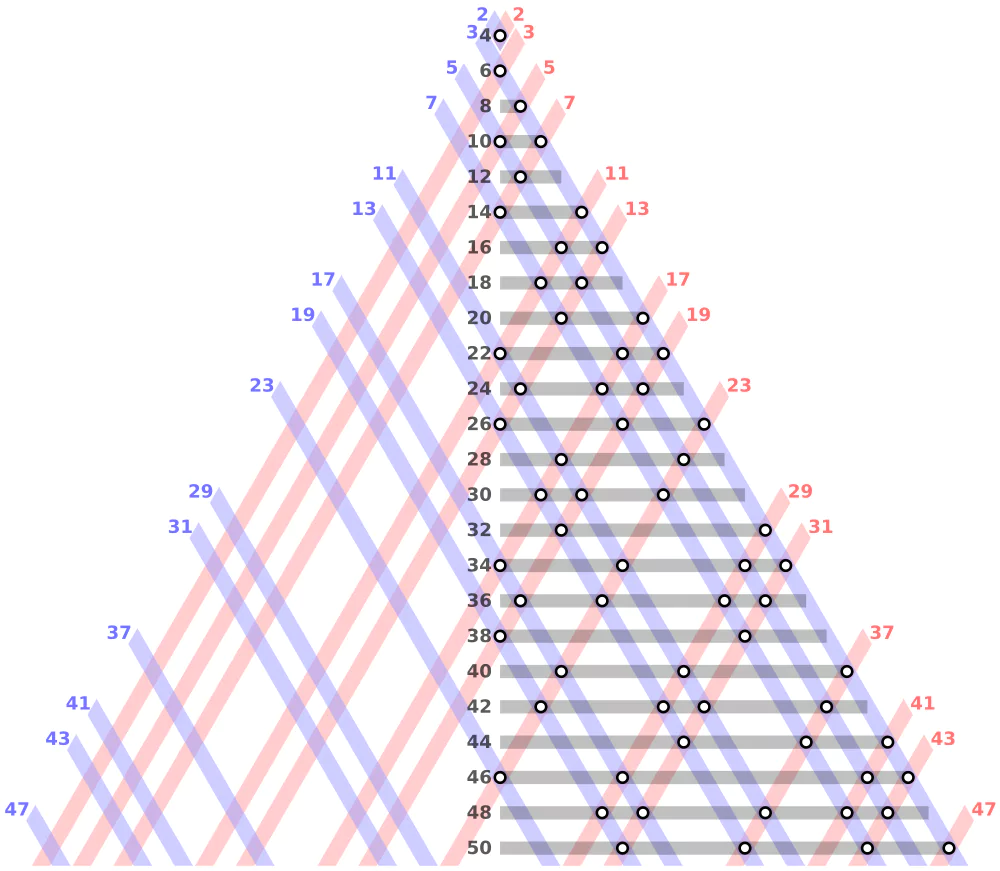
Despite extensive efforts by mathematicians, an analytic proof for the Goldbach Conjecture remains elusive. While the conjecture has been verified for numerous even integers, a rigorous proof that applies to all cases is yet to be discovered. The distribution of prime numbers provides an informal justification for the conjecture, as larger integers are more likely to be expressed as the sum of two primes.

The Inscribed Square Problem

The Inscribed Square Problem poses a fascinating question: Can any closed, non-intersecting curve contain four points that form a square? Mathematicians have explored this problem in various contexts, examining different types of curves and their relationship to inscribable squares.

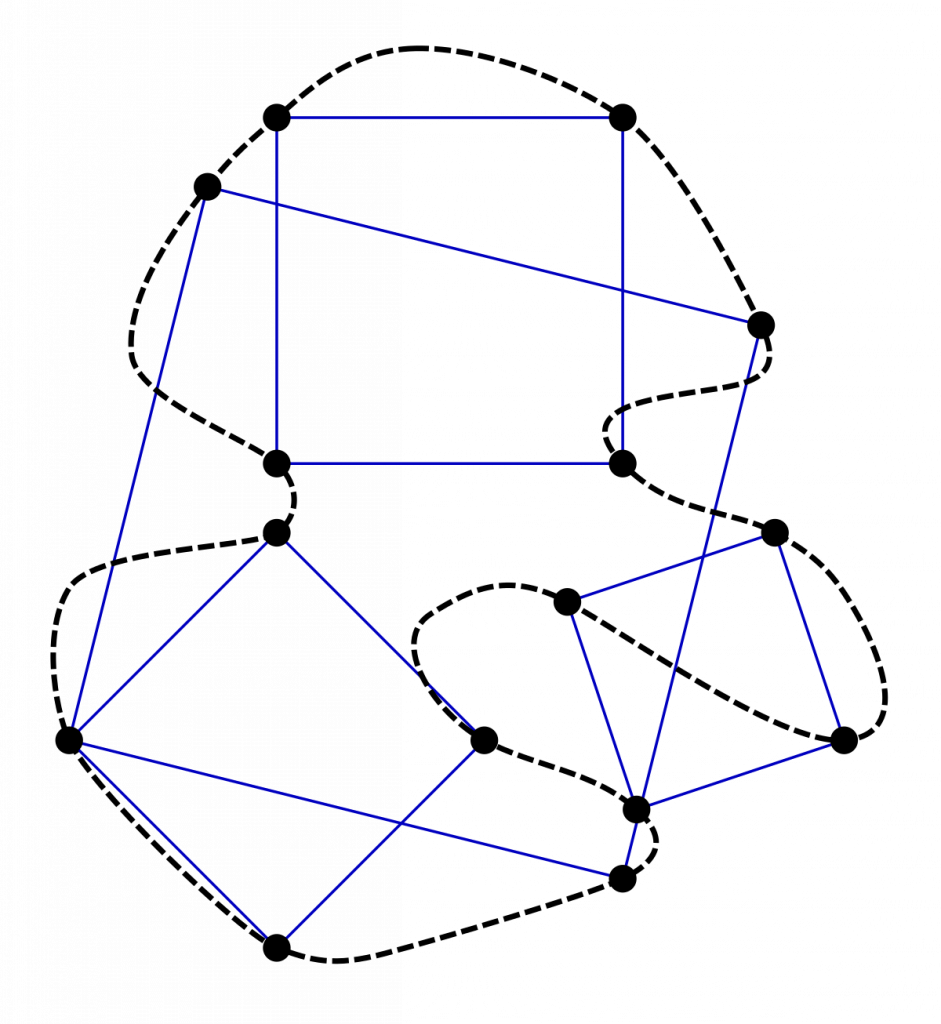
While the general case of the Inscribed Square Problem remains unsolved, specific instances have been proven. For example, it has been established that circles and squares have an infinite number of inscribable squares. Obtuse triangles have exactly one, while right and acute triangles have two and three inscribable squares, respectively.

The Continuum Hypothesis

The Continuum Hypothesis delves into the vast realm of infinities. In mathematics, different magnitudes of infinity exist, depending on the size and nature of the sets involved. Countable infinities, represented by sets that can be put into a 1-to-1 correspondence with the positive whole numbers, are distinct from uncountable infinities.

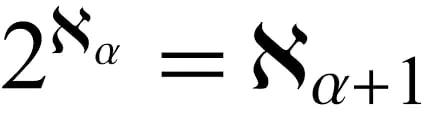
Georg Cantor’s work in the 19th century revealed that the set of real numbers is uncountable, meaning it cannot be paired with the positive whole numbers in a one-to-one manner. The Continuum Hypothesis asks whether there exists an infinity that falls between the countable and uncountable infinities. However, current mathematical techniques cannot solve or disprove this hypothesis, as it requires a new framework for set theory.

The Collatz Conjecture

The Collatz Conjecture presents a deceptively simple problem with intriguing complexity. It involves constructing an iterative sequence based on a positive number. If the number is even, divide it by 2; if it’s odd, multiply it by 3 and add 1. The conjecture claims that regardless of the starting value, this sequence will eventually reach the number 1.

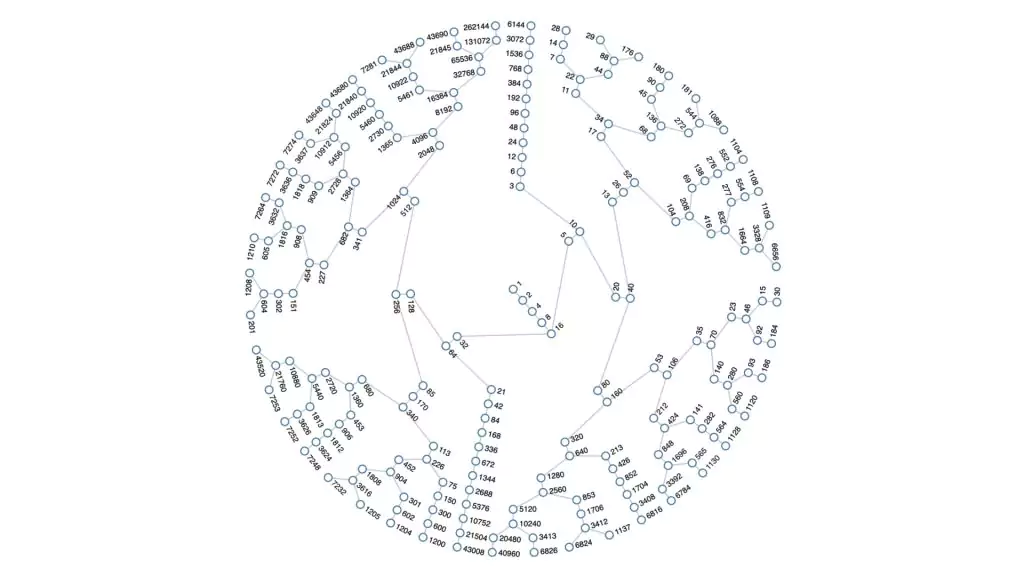
Exploring the Collatz Conjecture through examples can provide insights into its captivating nature. Starting with the number 12, we have the sequence: 12, 6, 3, 10, 5, 16, 8, 4, 2, 1. Similarly, beginning with 19, we get: 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. Despite extensive exploration, no pattern or proof has been found to support or disprove the conjecture.

Solving Chess

Solving Chess involves finding an optimal strategy that guarantees victory in every game. While optimal strategies have been discovered for simpler games like connect-4 and tic-tac-toe, the complexity of chess presents an immense challenge. The vast number of possible game variations makes it computationally infeasible to exhaustively search for an optimal move.

To tackle the complexity of chess, researchers have developed powerful artificial intelligence (AI) systems. These AI systems, like Deep Blue and AlphaZero, utilize advanced algorithms and neural networks to analyze vast amounts of data and identify winning strategies. However, it is important to note that these AI systems do not solve chess in the traditional sense but rely on extensive computational power and data analysis.

The Riemann Hypothesis

The Riemann Hypothesis, proposed by Bernhard Riemann in 1859, holds immense importance in the field of number theory. It focuses on the distribution of non-trivial zeros of the Riemann zeta function, a mathematical function with significant applications in various areas of mathematics.

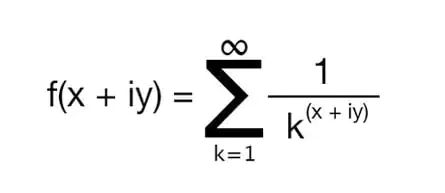
The Riemann Hypothesis’s profound implications extend beyond number theory, with connections to prime number distribution and the behavior of mathematical functions. Despite its fundamental importance, mathematicians have yet to prove or disprove the hypothesis. Its complexity and the absence of a definitive proof have earned it the status of one of the most challenging unsolved problems in mathematics.

Conclusion

The hardest math problems continue to enthrall mathematicians worldwide, pushing the boundaries of human knowledge and understanding. From the eternal quest to prove the Goldbach Conjecture and the intricacies of inscribed squares to the enigma of the Riemann Hypothesis, these problems symbolize the relentless pursuit of truth and the allure of the unknown. As mathematicians persist in their exploration, the mysteries of these problems remain unsolved, fueling curiosity and inspiring future generations to tackle the most challenging mathematical puzzles.

You can find more STEM Guides in our designated category here at A*Help!

FAQ

Related

A*Help Insights - sign up for our Newsletter

Sign up

Thanks for signing up!

Something went wrong. Please try again later.

Follow us on Reddit for more insights and updates.