A matemática sempre foi um reino de maravilhas, onde a busca de soluções para problemas complexos intrigou e cativou os estudiosos durante séculos. Neste guia, mergulhamos no mundo dos problemas matemáticos mais difíceis, explorando suas complexidades e a busca contínua por suas soluções. Desde a enigmática Conjectura de Goldbach até a elusiva Hipótese de Riemann, cada problema apresenta seus desafios exclusivos, inspirando os matemáticos a ultrapassar os limites da compreensão humana. Para aqueles que se sentem fascinados, mas perplexos com esses problemas complexos, buscar ajuda dos melhores serviços de tutoria on-line pode ser uma excelente maneira de se aprofundar nos problemas.

A Conjectura de Goldbach
A Conjectura de Goldbach, formulada por Christian Goldbach em 1742, é um quebra-cabeça matemático que gira em torno da expressão de números pares como a soma de dois números primos. A Conjectura de Goldbach é considerada um dos problemas matemáticos mais difíceis. Por exemplo, o número 10 pode ser expresso como 7 + 3, em que 7 e 3 são números primos.
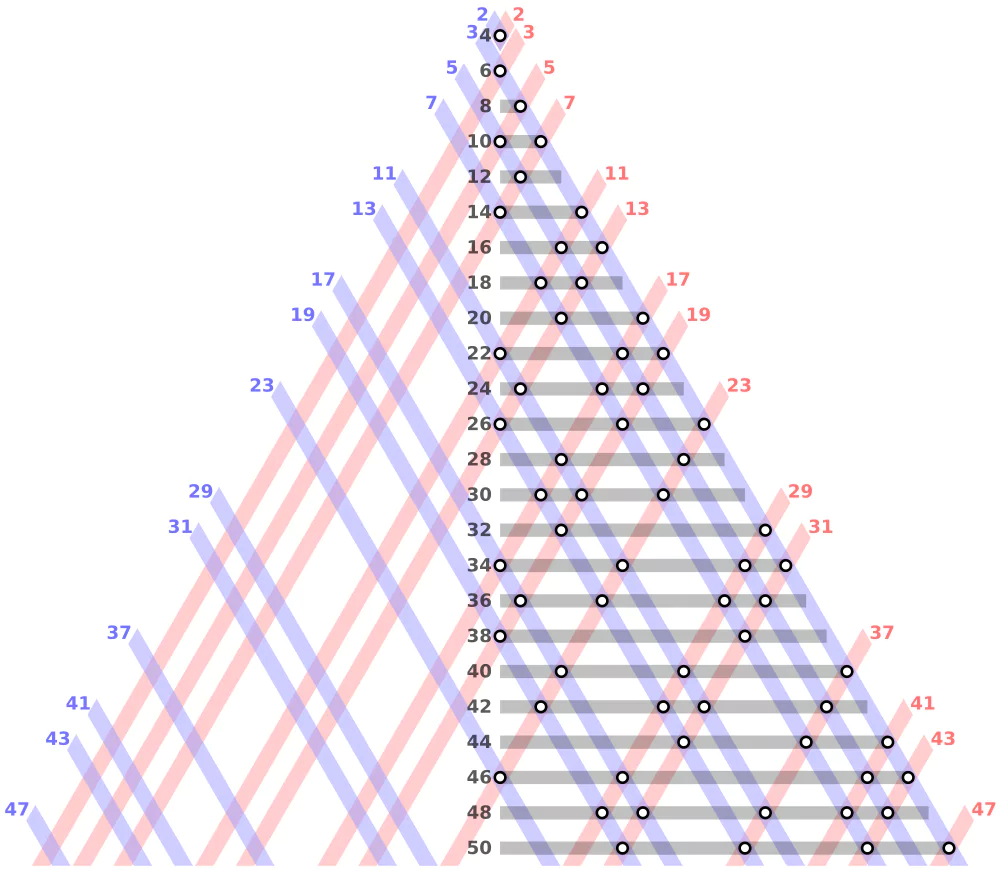
Apesar dos grandes esforços dos matemáticos, uma prova analítica para a Conjectura de Goldbach continua sendo difícil de ser obtida. Embora a conjectura tenha sido verificada para vários números inteiros pares, ainda não foi descoberta uma prova rigorosa que se aplique a todos os casos. A distribuição de números primos fornece uma justificativa informal para a conjectura, pois os números inteiros maiores têm maior probabilidade de serem expressos como a soma de dois números primos.
O Problema do Quadrado Inscrito
O Problema do Quadrado Inscrito apresenta uma questão fascinante: Qualquer curva fechada, sem interseção, pode conter quatro pontos que formam um quadrado? Os matemáticos exploraram esse problema em vários contextos, examinando diferentes tipos de curvas e sua relação com os quadrados inscritíveis.
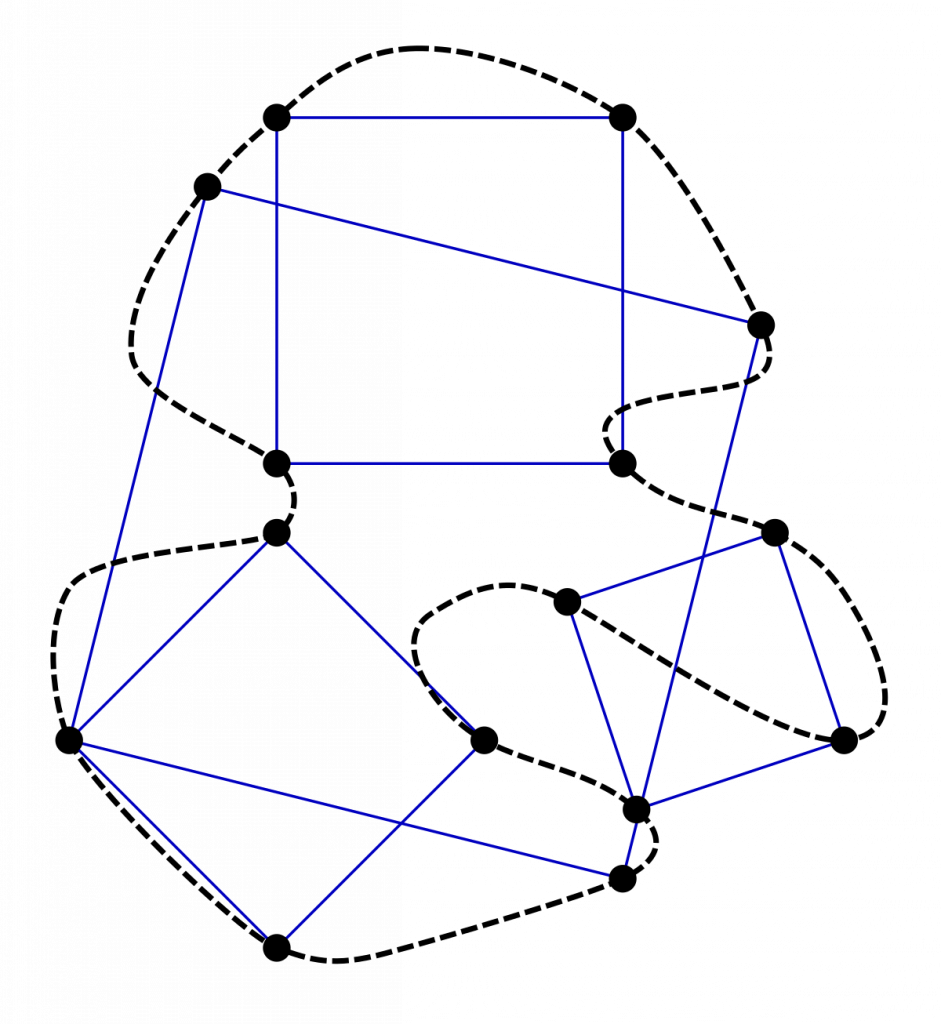
Embora o caso geral do Problema do Quadrado Inscrito permaneça sem solução, casos específicos foram comprovados. Por exemplo, foi estabelecido que os círculos e os quadrados têm um número infinito de quadrados inscritíveis. Os triângulos oblíquos têm exatamente um, enquanto os triângulos retos e agudos têm dois e três quadrados inscritíveis, respectivamente.
A Hipótese do Continuum
A Hipótese do Contínuo investiga o vasto reino dos infinitos. Na matemática, existem diferentes magnitudes de infinito, dependendo do tamanho e da natureza dos conjuntos envolvidos. Os infinitos contáveis, representados por conjuntos que podem ser colocados em uma correspondência de 1 para 1 com os números inteiros positivos, são diferentes dos infinitos incontáveis.
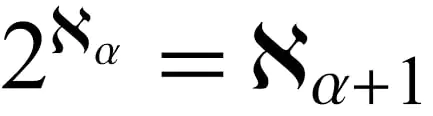
O trabalho de Georg Cantor no século XIX revelou que o conjunto de números reais é incontável, o que significa que não pode ser emparelhado com os números inteiros positivos de maneira individual. A Hipótese do Contínuo pergunta se existe um infinito entre os infinitos contáveis e incontáveis. Entretanto, as técnicas matemáticas atuais não podem resolver ou refutar essa hipótese, pois ela exige uma nova estrutura para a teoria dos conjuntos.
A Conjectura de Collatz
A Conjectura de Collatz apresenta um problema aparentemente simples com uma complexidade intrigante. Ela envolve a construção de uma sequência iterativa com base em um número positivo. Se o número for par, divida-o por 2; se for ímpar, multiplique-o por 3 e some 1. A conjectura afirma que, independentemente do valor inicial, essa sequência acabará chegando ao número 1.
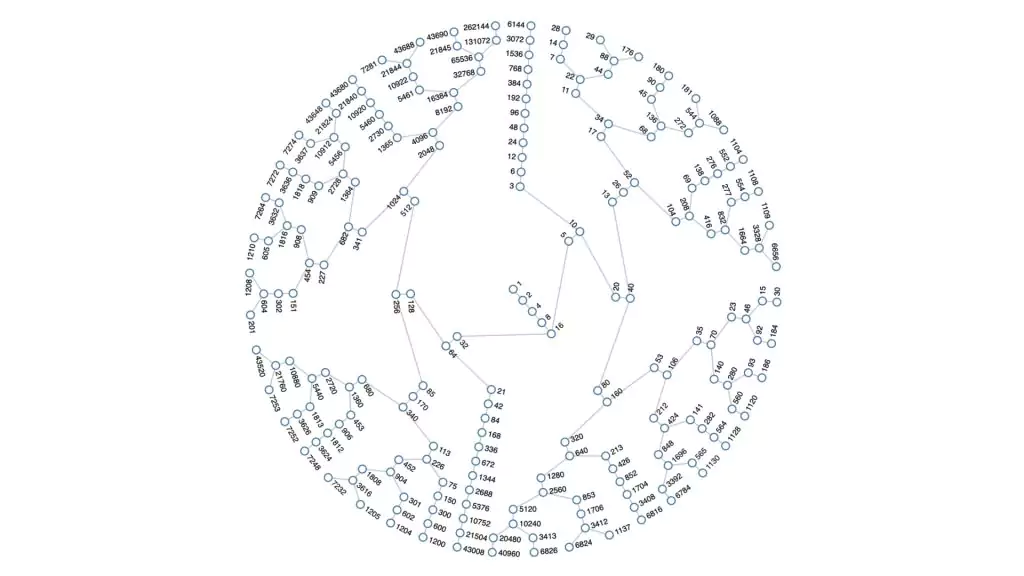
A exploração da Conjectura de Collatz por meio de exemplos pode fornecer informações sobre sua natureza cativante. Começando com o número 12, temos a sequência: 12, 6, 3, 10, 5, 16, 8, 4, 2, 1. Da mesma forma, começando com 19, temos: 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. Apesar da exploração extensiva, nenhum padrão ou prova foi encontrado para apoiar ou refutar a conjectura.
Resolvendo o Xadrez
A solução do xadrez envolve encontrar uma estratégia ideal que garanta a vitória em todos os jogos. Embora estratégias ótimas tenham sido descobertas para jogos mais simples, como o jogo da velha e o jogo do galo, a complexidade do xadrez representa um imenso desafio. O grande número de variações possíveis do jogo torna computacionalmente inviável a busca exaustiva de uma jogada ideal.
Para lidar com a complexidade do xadrez, os pesquisadores desenvolveram poderosos sistemas de inteligência artificial (IA). Esses sistemas de IA, como o Deep Blue e o AlphaZero, utilizam algoritmos avançados e redes neurais para analisar grandes quantidades de dados e identificar estratégias vencedoras. No entanto, é importante observar que esses sistemas de IA não resolvem o xadrez no sentido tradicional, mas dependem de grande capacidade computacional e análise de dados.
A Hipótese de Riemann
A Hipótese de Riemann, proposta por Bernhard Riemann em 1859, tem imensa importância no campo da teoria dos números. Ela se concentra na distribuição de zeros não triviais da função zeta de Riemann, uma função matemática com aplicações significativas em várias áreas da matemática.
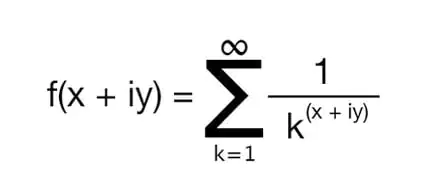
As profundas implicações da Hipótese de Riemann vão além da teoria dos números, com conexões com a distribuição de números primos e o comportamento das funções matemáticas. Apesar de sua importância fundamental, os matemáticos ainda não conseguiram provar ou refutar a hipótese. Sua complexidade e a ausência de uma prova definitiva lhe renderam o status de um dos mais desafiadores problemas não resolvidos da matemática.
Conclusão
Os problemas matemáticos mais difíceis continuam a encantar os matemáticos do mundo todo, ampliando os limites do conhecimento e da compreensão humana. Desde a eterna busca para provar a Conjectura de Goldbach e as complexidades dos quadrados inscritos até o enigma da Hipótese de Riemann, esses problemas simbolizam a busca incessante pela verdade e o fascínio do desconhecido. Como os matemáticos persistem em sua exploração, os mistérios desses problemas permanecem sem solução, alimentando a curiosidade e inspirando as gerações futuras a enfrentar os quebra-cabeças matemáticos mais desafiadores.
FAQ
Siga-nos em Reddit para obter mais informações e atualizações.




Comentários (0)
Bem-vindo aos comentários do A*Help!
Na A*Help, o que importa é o debate e a discussão.
Valorizamos as diversas opiniões dos usuários, portanto, você poderá encontrar pontos de vista com os quais não concorda. E isso é legal. No entanto, há certas coisas com as quais não concordamos: tentativas de manipular nossos dados de alguma forma, por exemplo, ou a publicação de material discriminatório, ofensivo, odioso ou depreciativo.