Momentum Essay Sample, Example

A conserved quantity of motion

Your first encounter with the conservation of momentum may have come as a small child unjustly confined to a shopping cart. You spot something interesting to play with, like the display case of imported wine down at the end of the aisle, and decide to push the cart over there. But being imprisoned by Dad in the cart was not the only injustice that day. There was a far greater conspiracy to thwart your young identity, one that originated in the laws of nature. Pushing forward did nudge the cart forward, but it pushed you backward. If the wheels of the cart were well lubricated, it would not matter how you jerked, yanked, or kicked off from the back of the cart. You could not cause any overall forward motion of the entire system consisting of the cart with you inside.

In Newtonian framework, we describe this as arising from Newton’s third law. The cart made a force on you that was equal and opposite to your force on it. In the framework of conservation laws, we cannot attribute your frustration to conservation of energy. It would have been perfectly possible for you to transform some of the internal chemical energy stored in your body to kinetic energy of the cart and your body.

The following characteristics of the situation suggest there may be a new conservation law involved:

A closed system is involved. All conservation laws deal with closed systems. You and the cart are a closed system, since the well-oiled wheels prevent the floor from making any forward force on you.

Something remains unchanged. The overall velocity of the system started out being zero, and you cannot change it. This vague reference to “overall velocity” can be made more precise: it is the velocity of the system’s center of mass that cannot be changed.

Something can be transferred back and forth without changing the total amount. If we define forward as positive and backward as negative, then one part of the system can gain positive motion if another part acquires negative motion. If we do not want to worry about positive and negative signs, we can imagine that the whole cart was initially gliding forward on its well-oiled wheels. By kicking off from the back of the cart, you could increase your own velocity, but this inevitably causes the cart to slow down.

It thus appears that there is some numerical measure of an object’s quantity of motion that is conserved when you add up all the objects within a system.

Momentum

Although velocity has been referred to, it is not the total velocity of a closed system that remains constant. If it was, then firing a gun would cause the gun to recoil at the same velocity as the bullet! The gun does recoil, but at a much lower velocity than the bullet. Newton’s third law tells us

Fgun on bullet=−Fbullet on gun,

and assuming a constant force for simplicity, Newton’s second law allows us to change this to

mbulletΔvbulletΔt=−mgunΔvgunΔt.

Thus, if the gun has 100 times more mass than the bullet, it will recoil at a velocity that is 100 times smaller and in the opposite direction, represented by the opposite sign. The quantity mvmv is therefore apparently a useful measure of motion, and we give it a name, momentum, and a symbol, pp. (as far as I know, the letter “p” was chosen at random, since “m” was already being used for mass). The situations discussed so far have been one-dimensional, but in three-dimensional situations it is treated as a vector.

Definition of momentum for material objects

The momentum of a material object, i.e., a piece of matter, is defined as

p=mv,

the product of the object’s mass and its velocity vector.

The units of momentum are kg⋅m/skg⋅m/s, and there is unfortunately no abbreviation for this clumsy combination of units.

The reasoning leading up to the definition of momentum was all based on the search for a conservation law, and the only reason why we bother to define such a quantity is that experiments show it is conserved:

the law of conservation of momentum

In any closed system, the vector sum of all the momenta remains constant,

p1i+p2i+…=p1f+p2f+…,

where ii labels the initial and ff the final momenta (a closed system is one on which no external forces act).

A subtle point about conservation laws is that they all refer to “closed systems,” but “closed” means different things in different cases. When discussing conservation of mass, “closed” means a system that does not have matter moving in or out of it. With energy, we mean there is no work or heat transfer occurring across the boundary of the system. For momentum conservation, “closed” means there are no external forces reaching into the system.

Example 1: A cannon

– A cannon of mass 1000 kg fires a 10-kg shell at a velocity of 200 m/s. At what speed does the cannon recoil?

– The law of conservation of momentum tells us that

pcannon,i+pshell,i=pcannon,f+pshell,f.

Choosing a coordinate system in which the cannon points in the positive direction, the given information is

pcannon,ipshell,ipshell,f=0=0=2000 kg⋅m/s.

We must have pcannon,f=−2000 kg⋅m/spcannon,f=−2000 kg⋅m/s, so the recoil velocity of the cannon is −2−2 m/s.

ion-drive

The ion drive engine of the NASA Deep Space 1 probe is under construction and being tested in a vacuum chamber prior to its October 1998 launch. Intended mainly as a test vehicle for new technologies, the craft nevertheless carried out a successful scientific program that included a flyby of a comet.

Example 2: Ion drive for propelling spacecraft

– The experimental solar-powered ion drive of the Deep Space 1 space probe expels its xenon gas exhaust at a speed of 30,000 m/s, ten times faster than the exhaust velocity for a typical chemical-fuel rocket engine. Roughly how many times greater is the maximum speed this spacecraft can reach, compared with a chemical-fueled probe with the same mass of fuel (“reaction mass”) available for pushing out the back as exhaust?

– Momentum equals mass multiplied by velocity. Both spacecraft are assumed to have the same amount of reaction mass, and the ion drive’s exhaust has a velocity ten times greater, so the momentum of its exhaust is ten times greater. Before the engine starts firing, neither the probe nor the exhaust has any momentum, so the total momentum of the system is zero. By conservation of momentum, the total momentum must also be zero after all the exhaust has been expelled. If we define the positive direction as the direction the spacecraft is going, then the negative momentum of the exhaust is canceled by the positive momentum of the spacecraft. The ion drive allows a final speed that is ten times greater (this simplified analysis ignores the fact that the reaction mass expelled later in the burn is not moving backward as fast, because of the forward speed of the already-moving spacecraft).

Generalization of the momentum concept

As with all the conservation laws, the law of conservation of momentum has evolved over time. In the 1800s, it was found that a beam of light striking an object would give it some momentum, even though light has no mass, and would therefore have no momentum according to the above definition. Rather than discarding the principle of conservation of momentum, the physicists of the time decided to see if the definition of momentum could be extended to include momentum carried by light. The process is analogous to the process outlined on page 295 for identifying new forms of energy. The first step was the discovery that light could impart momentum to matter, and the second step was to show that the momentum possessed by light could be related in a definite way to observable properties of the light. They found that the conservation of momentum could be successfully generalized by attributing to a beam of light a momentum vector in the direction of the light’s motion and having a magnitude proportional to the amount of energy the light possessed. The momentum of light is negligible under ordinary circumstances, e.g., a flashlight left on for an hour would only absorb about 10−5 kg⋅m/s10−5 kg⋅m/s of momentum as it recoiled.

Example 3: The tail of a comet

Momentum is not always equal to mvmv. Like many comets, Halley’s comet has a very elongated elliptical orbit. About once per century, its orbit brings it close to the sun. The comet’s head, or nucleus, is composed of dirty ice, so the energy deposited by the intense sunlight boils off steam and dust, b. The sunlight does not just carry energy, however—it also carries momentum. The momentum of the sunlight impacting on the smaller dust particles pushes them away from the sun, forming a tail, c. By analogy with matter, for which momentum equals mvmv, you would expect that massless light would have zero momentum, but the equation p=mvp=mv is not the correct one for light, and light does have momentum (the gases typically form a second, distinct tail whose motion is controlled by the sun’s magnetic field).

The reason for bringing this up is not so that you can plug numbers into a formulas in these exotic situations. The point is that the conservation laws have proven so sturdy exactly because they can easily be amended to fit new circumstances. Newton’s laws are no longer at the center of the stage of physics because they did not have the same adaptability. More generally, the moral of this story is the provisional nature of scientific truth.

It should also be noted that conservation of momentum is not a consequence of Newton’s laws, as is often asserted in textbooks. Newton’s laws do not apply to light, and therefore could not possibly be used to prove anything about a concept as general as the conservation of momentum in its modern form.

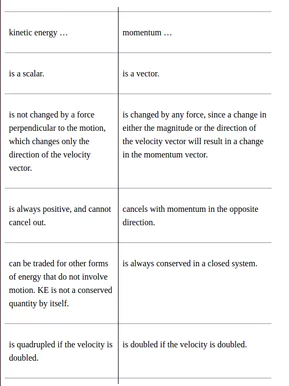
Momentum compared to kinetic energy

Momentum and kinetic energy are both measures of the quantity of motion, and a sideshow in the Newton-Leibnitz controversy over who invented calculus was an argument over whether mv (i.e., momentum) or mv2mv2 (i.e., kinetic energy without the 1/2 in front) was the “true” measure of motion. The modern student can certainly be excused for wondering why we need both quantities, when their complementary nature was not evident to the greatest minds of the 1700s. The following table highlights their differences.

A*Help Insights - sign up for our Newsletter

Sign up

Thanks for signing up!

Something went wrong. Please try again later.

Follow us on Reddit for more insights and updates.