How to Find the Y Intercept with Two Points: Explained

Understanding how to find the y-intercept of a line when given two points is a fundamental concept in algebra and coordinate geometry. This process involves using the slope-intercept form of a linear equation. In this article, we will explore the step-by-step method to calculate the y-intercept using two points, incorporating key concepts such as slope, equation of the line, and the significance of the y-intercept.

JOIN OUR LEARNING HUB

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator

Get Free Tools

Understanding the Basics

The slope-intercept form of a linear equation is given by y=mx+b, where m is the slope and b is the y-intercept. This form is particularly useful as it directly relates the slope and y-intercept with the linear equation of the graph.

Significance of the Y-Intercept

The y-intercept is the point where the line intersects the Y-axis. This value is crucial as it indicates the point at which the value of x is zero. Understanding the y-intercept helps in graphically representing the equation and in understanding the behavior of the line.

Calculating the Slope

To find the y-intercept using two points, we first need to calculate the slope (m). Consider two points on the line, for example, (3, 5) and (6, 11). The slope is calculated using the formula:

How to Find the Y-Intercept with Two Points

Example:

For the points (3, 5) and (6, 11), the slope m is calculated as:

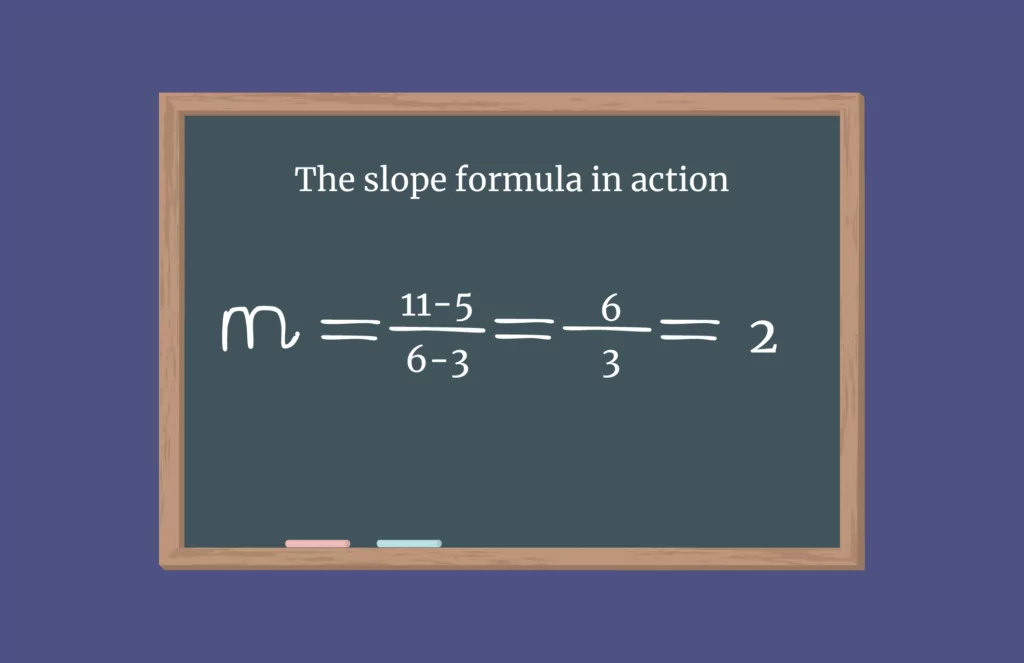
Once the slope is determined, the next step is to find the y-intercept, b.

Using Slope-Intercept Form

Substitute the slope (m) into the slope-intercept form y=mx+b and use one of the given points to solve for b.

Solve for b

Let’s use the point (3, 5) and the calculated slope m=2:

5=2(3)+b

5=6+b

b=5−6

b=−1

So, the y-intercept b is -1.

Graphical Representation

Understanding the graphical aspect is essential. The point where the line crosses the Y-axis is the y-intercept. In our example, this point would be (0, -1).

Conclusion

Finding the y-intercept with two points is a straightforward process involving calculating the slope using the point-slope formula and then substituting into the slope-intercept form to find b. This method is not only fundamental in algebra but also forms the basis for more complex calculations in calculus, like finding the tangent line at a given point. Remember, the y-intercept is a key feature in understanding the graph of a linear equation.

Additional Considerations

While the focus of this article is on finding the y-intercept using two points, it’s important to note that this method can also be used to solve for other variables in the equation or to find the equation of a tangent line in calculus. The core concepts of slope, y-intercept, and the linear equation form the foundation for these advanced applications.

FAQ

What is the Y-intercept in Mathematics?

The y-intercept in mathematics refers to the point where a line, curve, or surface intersects the y-axis of a coordinate system. In the context of a linear equation, it is the point at which the line crosses the y-axis. This point represents the value of y when x is equal to zero. In the equation of a line in slope-intercept form, which is y=mx+b, the y-intercept is denoted by b. It is a critical component in graphing linear equations and understanding the behavior of linear functions.

Is the Y-intercept Important in Linear Equations?

Yes, the y-intercept is very important in linear equations. It provides essential information about the line represented by the equation, particularly where the line crosses the y-axis. This intercept is a key element in graphically representing the line and is crucial for understanding the relationship between the variables in the equation. For instance, in real-world scenarios, the y-intercept can represent a starting value or initial condition before any changes represented by the slope take place.

Are There Multiple Methods to Determine the Y-intercept?

Indeed, there are multiple methods to determine the y-intercept. While the method of using two points to calculate the slope and then finding the y-intercept is common, other methods also exist. One can directly read off the y-intercept from an equation in slope-intercept form. If the equation is in a different form, such as standard form (ax+by=c), rearranging the equation to the slope-intercept form can reveal the y-intercept. Additionally, graphical methods can be used where the line is plotted, and the y-intercept is determined visually where the line crosses the y-axis.

How Do You Graph Linear Equations with Two Points?

To graph linear equations using two points, you first plot the two given points on the coordinate plane. After plotting these points, use them to calculate the slope of the line, which is the rate at which y changes with respect to x. Once the slope is determined, you can use one of the points and the slope to find the y-intercept of the line, which is where the line crosses the y-axis. With the slope and y-intercept, you can draw the line that passes through the two points. This process visualizes the linear relationship depicted by the equation, showing how the value of y varies with x.

ALGEBRA

Opt out or Contact us anytime. See our Privacy Notice

Comments (0)

Welcome to A*Help comments!

We’re all about debate and discussion at A*Help.

We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.

Most Popular

How to Find the Y-Intercept with Two Points