In the realm of mathematics, the concept of congruence plays a vital role in understanding the relationship between geometric figures. Congruent figures possess identical shapes and sizes, allowing for precise placement and comparison. This article explores the meaning of congruence in math, provides insightful examples, and delves into its significance in various mathematical contexts.

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
What Does Congruent Mean in Math?
When we say two figures are congruent, we mean that they can be precisely placed over each other, resulting in a perfect match of shape and size. In mathematics, the term “congruent” indicates an exact equality between two figures. This equality remains consistent, regardless of flipping, turning, or rotating the figures.
Examples of Congruent Figures
To understand the concept of congruence better, let’s explore a few examples of congruent figures in everyday life. Two butterflies with the same shape and size, two candy ice creams representing equal proportions, and two Lego bricks exhibiting identical dimensions are all examples of congruent figures. These examples highlight how congruence manifests in objects around us.

In mathematical notation, congruence is denoted by the symbol ‘≅’. This symbol is composed of two parts: the tilde symbol ‘∼’ signifies similarity in shape, while the equals sign ‘=’ represents equality in size. Hence, when two objects A and B are congruent, we express it as A ≅ B.
Congruent Line Segments
Congruent line segments share the same shape and size. Consider line segments AB and PQ. If the length of AB is 5 cm and the length of PQ is also 5 cm, we can conclude that both line segments are congruent. Mathematically, we represent this relationship as line segment AB ≅ line segment PQ.
Congruent Angles
In geometry, congruent angles have equal measures. Let’s take the example of angles ∠ABC and ∠PQR. If ∠ABC measures 40° and ∠PQR also measures 40°, we can superimpose or overlap these angles to observe their congruence. Consequently, we can express the congruence of these angles as ∠ABC ≅ ∠PQR.
Congruent Circles
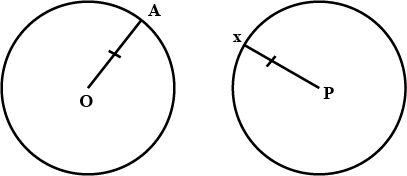
Congruent circles possess the same shape and size. Consider Circle A with a radius represented by OR and Circle B with a radius represented by OP. If the lengths of radii OR and OP are both 2 cm, we conclude that Circle A is congruent to Circle B. Mathematically, we express this congruence as Circle A ≅ Circle B.
Congruent Triangles
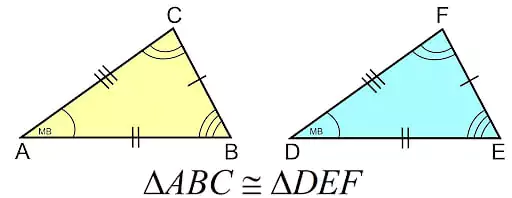
For triangles to be congruent, all three sides and all three angles must be congruent. Consider triangles ABC and EFG. If we observe that side AC is equal to side EG, side AB is equal to side EF, and side BC is equal to side FG, along with the congruence of corresponding angles (e.g., ∠A ≅ ∠E), we can conclude that triangles ABC ≅ EFG. This relationship between congruent triangles is governed by the rule of Corresponding Parts of Congruent Triangles (CPCT).
Difference between Congruent Figures and Similar Figures
It is important to distinguish between congruent figures and similar figures. While both share similarities in shape, the key difference lies in the equality of corresponding angles and the lengths of corresponding sides. Congruent figures exhibit equality in both angles and side lengths, while similar figures only have equal corresponding angles. The lengths of their corresponding sides may differ.
Conclusion
Congruence is a fundamental concept in mathematics that allows us to establish relationships between geometric figures. Understanding congruence helps us analyze and compare shapes, sizes, and angles accurately. By exploring examples and applications of congruence, we have gained a deeper comprehension of its significance in various mathematical contexts.
FAQ
What are some examples of congruent shapes in real life?
Congruent shapes can be found in various objects around us. Here are a few examples:
- Two butterflies with identical shapes and sizes
- Two candy ice creams representing equal proportions
- Two Lego bricks exhibiting the same dimensions
- Two mirrors that are exact replicas of each other
How is congruence represented in mathematical symbols?
Congruence is represented by the symbol ‘≅’ in mathematics. This symbol consists of two parts: the tilde symbol ‘∼’ represents similarity in shape, while the equals sign ‘=’ denotes equality in size. When two objects or figures are congruent, we express it as A ≅ B.
Are congruent line segments always of the same length?
Yes, congruent line segments are always of the same length. Congruence implies that two line segments have identical shapes and sizes. If two line segments are congruent, it means that their lengths are equal. The equality of length is a fundamental property of congruent line segments.
Follow us on Reddit for more insights and updates.





Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.