What is beta in Statistics

In the world of finance and investment, understanding the concept of beta is crucial for assessing risk and evaluating the volatility of securities. Beta serves as a statistical measure that helps investors comprehend how a particular security or portfolio behaves in relation to the overall market. This article will delve into the definition, calculation, and practical implications of beta, shedding light on its significance in statistical analysis and investment decision-making.

Defining Beta

The Measure of Volatility and Risk Beta, often denoted as β, is a statistical measure used in finance to assess the volatility and risk associated with a security or portfolio. It measures the sensitivity of the security’s returns to the overall market returns. In other words, beta provides insight into how much a security’s price tends to move in response to fluctuations in the market. For those studying finance and finding concepts like beta complex, it may be tempting to pay someone to do my statistics homework to gain a deeper understanding of these topics.

Calculation and Interpretation of Beta

To calculate beta, statistical regression analysis is used. This involves comparing the historical returns of the security to the historical returns of a benchmark, typically a market index such as the S&P 500. The formula for beta is as follows:

Beta coefficient (β) = Covariance (Return of the security, Return of the market) / Variance (Return of the market)

In this formula, the covariance represents how the returns of the security are related to the returns of the market. It measures the extent to which the security’s returns move in the same direction as the market returns. A positive covariance indicates a positive relationship, while a negative covariance suggests an inverse relationship.

The variance, on the other hand, measures how far the market’s data points spread out from their average value. It provides a measure of the overall volatility of the market returns. A higher variance indicates greater market volatility, while a lower variance suggests lower volatility.

By dividing the covariance by the variance, we obtain the beta coefficient. This coefficient represents the sensitivity of the security’s returns to changes in the market returns. A beta value greater than 1 indicates that the security is more volatile than the market, while a beta value less than 1 suggests lower volatility compared to the market.

Interpreting beta values allows investors to assess the risk and volatility of a security relative to the market. A beta equal to 1 indicates that the security moves in line with the market and has a similar level of volatility. Beta values greater than 1 indicate higher volatility, meaning the security tends to experience larger price swings in response to market fluctuations. Conversely, beta values less than 1 suggest lower volatility, indicating that the security has smaller price movements compared to the market.

It’s important to note that beta is a historical measure based on past data. The calculated beta reflects the relationship between the security’s returns and the market’s returns up to the period analyzed. As such, beta should be interpreted with caution and considered in conjunction with other factors when assessing the risk and potential returns of a security.

Interpreting beta values:

1. Beta Equal to 1.0: A beta value of 1.0 indicates that the security moves in line with the market. It has a similar level of volatility and risk as the overall market.
2. Beta Less Than One: A beta value less than 1.0 implies that the security is less volatile than the market. It tends to have smaller price movements compared to the market.
3. Beta Greater Than One: A beta value greater than 1.0 suggests that the security is more volatile than the market. It tends to experience larger price swings in response to market fluctuations.
4. Negative Beta Values: Negative beta values indicate an inverse relationship with the market. This means the security moves in the opposite direction of the market. It may act as a hedge against market downturns.

Beta and Risk Assessment

Beta is widely used in risk assessment and portfolio management. It provides insights into the systematic risk of a security, which is the risk associated with the overall market rather than specific factors affecting the individual security. By considering beta, investors can assess the potential risk and return characteristics of a security or portfolio.

Practical Application of Beta

Beta has various practical applications in portfolio construction, risk management, and the comparison of securities. By utilizing beta, investors can make informed decisions that align with their risk tolerance and financial goals. Some specific applications include:

1. Portfolio Construction: Beta can be used to construct diversified portfolios that align with an investor’s risk tolerance. By combining securities with different beta values, investors can achieve a balance between risk and potential returns. For example, including securities with low beta values can provide stability to the portfolio during market downturns, while securities with high beta values can offer the potential for higher returns during bullish market conditions.
2. Risk Management: Beta helps investors identify the risk associated with individual securities and the overall portfolio. By assessing the beta of each security, investors can evaluate the potential losses they may face during market downturns. Securities with higher beta values are likely to experience larger price fluctuations, indicating higher risk. This information can be used to manage portfolio risk by diversifying across securities with different beta values or adjusting the portfolio’s allocation based on the desired risk exposure.
3. Comparison of Securities: Beta enables investors to compare the risk and volatility of different securities. By analyzing beta values, investors can identify securities that may provide higher potential returns but also carry higher risks. For example, a security with a beta greater than 1.0 is expected to have higher volatility than the market, indicating the potential for larger price movements in both directions. On the other hand, a security with a beta less than 1.0 is expected to have lower volatility compared to the market. This information can assist investors in evaluating and selecting securities that align with their risk-reward preferences.

It’s important to note that while beta provides insights into risk and volatility, it should not be the sole determinant for investment decisions. Other factors such as fundamental analysis, financial ratios, and qualitative considerations should also be taken into account. Beta should be used in conjunction with other tools and metrics to form a comprehensive investment strategy.

By incorporating beta analysis into portfolio construction, risk management, and security comparison, investors can make more informed decisions, optimize risk-reward trade-offs, and align their investments with their financial objectives. It provides a valuable tool for understanding the risk characteristics of securities and portfolios, ultimately aiding in achieving long-term investment success.

Limitations of Beta

It’s important to acknowledge the limitations of beta as a measure of risk. Beta is based on historical data and assumes that the future behavior of the security will resemble the past. However, market conditions and other factors may change, rendering historical beta less reliable. Additionally, beta only considers the relationship between the security and the market, neglecting company-specific factors and events that may impact the security’s performance.

Factors Affecting Beta

Several factors can influence a security’s beta value, including industry dynamics, economic conditions, and company-specific characteristics. For example, companies operating in highly cyclical industries may exhibit higher beta values as their performance is more closely tied to economic fluctuations. On the other hand, defensive sectors such as utilities or consumer staples may have lower beta values as their earnings tend to be more stable.

Beta and Market Efficiency

The concept of beta is closely related to the efficient market hypothesis (EMH), which suggests that financial markets quickly and accurately incorporate all available information into security prices. In an efficient market, the beta of a security should reflect all relevant information about its risk and return potential.

Beta plays a significant role in the Capital Asset Pricing Model (CAPM), a widely used framework for pricing risky securities and estimating expected returns. CAPM utilizes beta to determine the appropriate required rate of return for a security based on its systematic risk.

In active portfolio management, where investors aim to outperform the market, beta is an important consideration. Portfolio managers often seek securities with high beta values during bullish market conditions to capitalize on upward movements. Conversely, during market downturns, low-beta securities may be favored to mitigate downside risk.

The Bottom Line

Beta is a valuable statistical measure in finance that provides insights into the volatility and risk of securities. By understanding and interpreting beta values, investors can make informed decisions, manage risk, and construct portfolios that align with their risk tolerance and financial goals. However, it’s important to use beta in conjunction with other analysis tools and consider its limitations to gain a comprehensive understanding of risk and make well-rounded investment decisions.

FAQ

How is beta interpreted in statistics?

Beta in statistics is interpreted as a measure of the sensitivity of a security or portfolio’s returns to changes in the overall market returns. A beta value greater than 1 indicates higher volatility than the market, while a value less than 1 suggests lower volatility. Beta equal to 1 signifies that the security moves in line with the market.

What is the significance of beta in regression analysis?

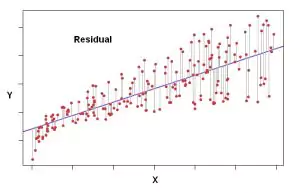
Beta plays a crucial role in regression analysis as it represents the slope of the regression line. In regression analysis, beta quantifies the relationship between a dependent variable and an independent variable. It provides insights into how a unit change in the independent variable affects the dependent variable.

How does beta relate to the slope of a regression line?

Beta is equivalent to the slope of a regression line in regression analysis. The beta coefficient measures the change in the dependent variable (Y) corresponding to a one-unit change in the independent variable (X). Thus, it indicates the rate of change in the dependent variable for each unit change in the independent variable.

Can beta values be used to compare different variables?

Beta values are specific to the relationship between a dependent variable and an independent variable in regression analysis. Therefore, beta values cannot be directly used to compare different variables or relationships. Each beta value represents the unique relationship between two variables in the specific regression model.

Is beta the only measure of the relationship between variables in regression analysis?

No, beta is not the only measure of the relationship between variables in regression analysis. While beta provides valuable information about the slope and direction of the relationship, other measures, such as R-squared and p-values, are also essential in assessing the strength and significance of the relationship. R-squared indicates the proportion of the dependent variable’s variation explained by the independent variable(s), while p-values assess the statistical significance of the relationship.

A*Help Insights - sign up for our Newsletter

Sign up

Thanks for signing up!

Something went wrong. Please try again later.

Follow us on Reddit for more insights and updates.