Triangles, the simplest polygons, are fundamental in geometry. Whether in construction or navigation, understanding how to find a triangle’s missing side length is crucial. This article will guide you through various methods to solve this mystery, focusing on different types of triangles and the Pythagorean Theorem.

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
Types of Triangles
When you’re trying to find a missing side length in a triangle, it’s super important to know what kind of triangle you’re working with. Each type has its own set of rules, and understanding these can make solving problems a whole lot easier.
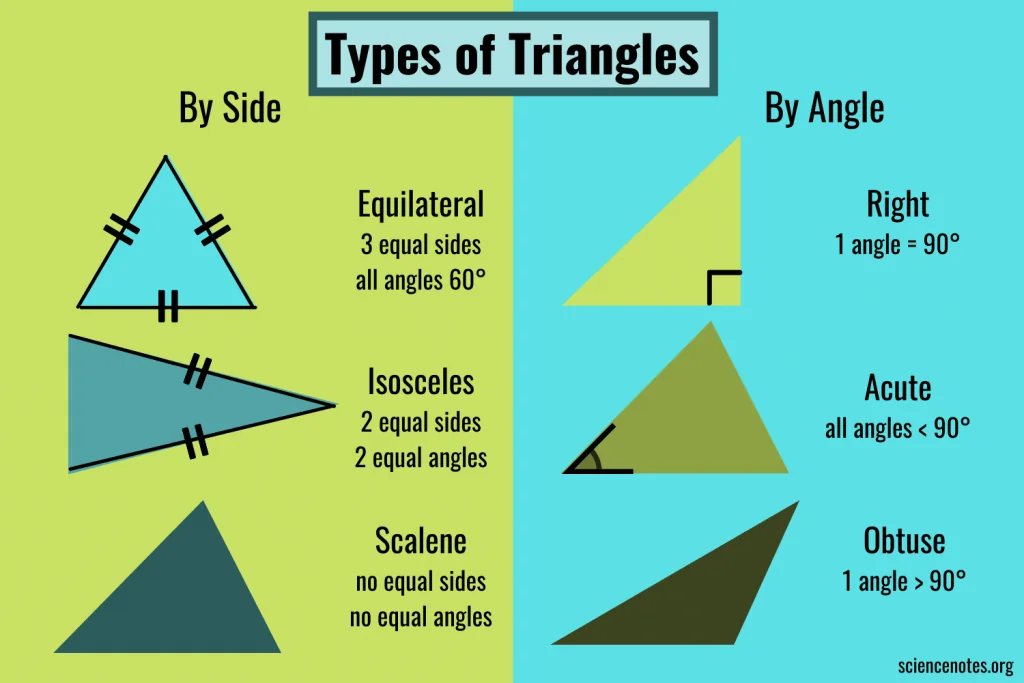
Let’s break down the different types:
- Right Triangle: Picture a triangle with one corner forming a perfect L shape – that’s your right triangle. It has one 90-degree angle, and the longest side, called the hypotenuse, is always opposite this right angle. Think of it as the “hero” side, stretching across from one corner to the other without touching the right angle.
- Equilateral Triangle: Imagine a triangle where all three sides are like triplets – they’re all exactly the same length. That’s your equilateral triangle. It’s the most balanced of all triangles, with each angle also being the same, at 60 degrees. It’s like the perfect harmony in the triangle world.
- Isosceles Triangle: This triangle is like a pair of best friends holding hands – it has two sides that are equal in length. These equal sides create a sense of symmetry, and the angles at the base of these sides are also equal. It’s like having a mirror line right down the middle.
- Scalene Triangle: Now, imagine a triangle where every side is doing its own thing – none of them are the same length. That’s your scalene triangle. It’s the most “independent” of the triangles, with all sides and angles being different from each other.
By knowing these types of triangles, you can approach problems with the right tools and strategies. Whether you’re dealing with the straightforward right triangle or the more complex scalene triangle, understanding their properties will help you find those missing sides with confidence!
Pythagorean Theorem
The Pythagorean Theorem is a superstar in the world of geometry, especially when it comes to right triangles. It’s named after the ancient Greek mathematician Pythagoras, who lived around 570–495 BCE. Pythagoras and his followers, the Pythagoreans, were fascinated by numbers and their relationships, and they discovered this geometric gem.
The beauty of the Pythagorean Theorem is that it applies to every right triangle, no matter the size or dimensions. It’s a universal truth in the world of geometry. This theorem not only helps you find missing side lengths but also has applications in various fields, such as physics, engineering, and computer science.
It’s like a magic formula that lets you find the missing piece of the puzzle. The theorem says that in a right triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b). In other words

To use the Pythagorean Theorem, you just need to know the lengths of two sides of a right triangle. If you’re looking for the hypotenuse, you add the squares of the other two sides and then take the square root of the result. If you’re looking for one of the other sides, you rearrange the equation to solve for that side.
How to Find the Missing Side Length of a Triangle That Isn’t Right
When you’re dealing with a triangle that isn’t a right triangle, things get a bit trickier, but don’t worry! We’ve got a couple of handy tools to help you out: the Law of Sines and the Law of Cosines. Let’s break down how you can use these tools to find that elusive missing side length:
Law of Sines
This law is all about the relationship between the lengths of the sides and the sines of the opposite angles. It’s like a bridge connecting angles and sides. The formula goes like this:
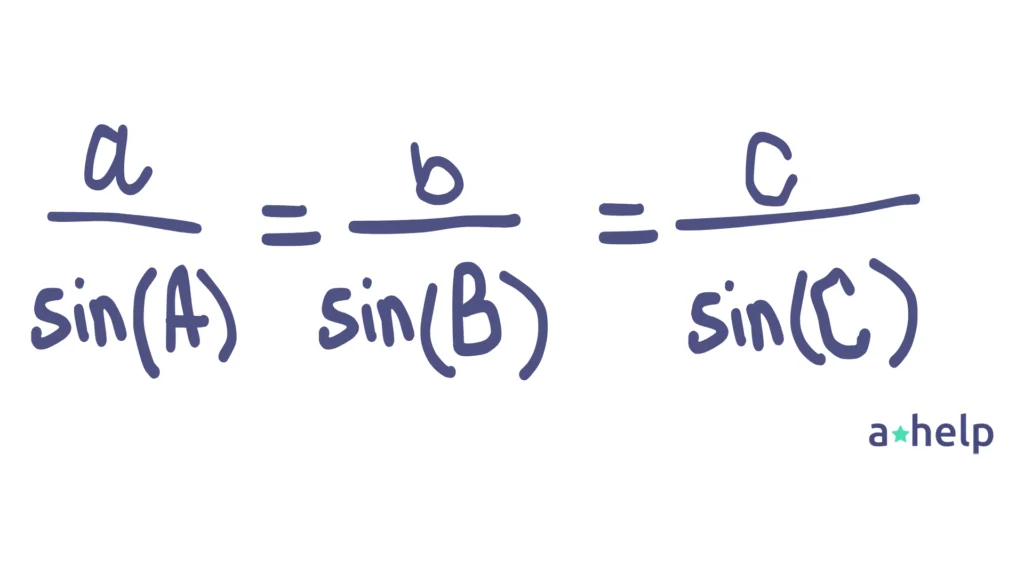
where a, b, and c are the sides, and A, B, and C are the angles opposite those sides.
When to use it: The Law of Sines is your best friend when you know:
- Two angles and one side (AAS or ASA) – In this case, you can use the known angles and sides to find the missing sides.
- Two sides and an angle opposite one of them (SSA) – Here, you can find the missing angle using the known sides and angle, and then use that to find the missing side.
Law of Cosines
This law is like an extension of the Pythagorean Theorem for all triangles. It helps you relate the sides of a triangle to the cosine of one of its angles. The formula looks like this:
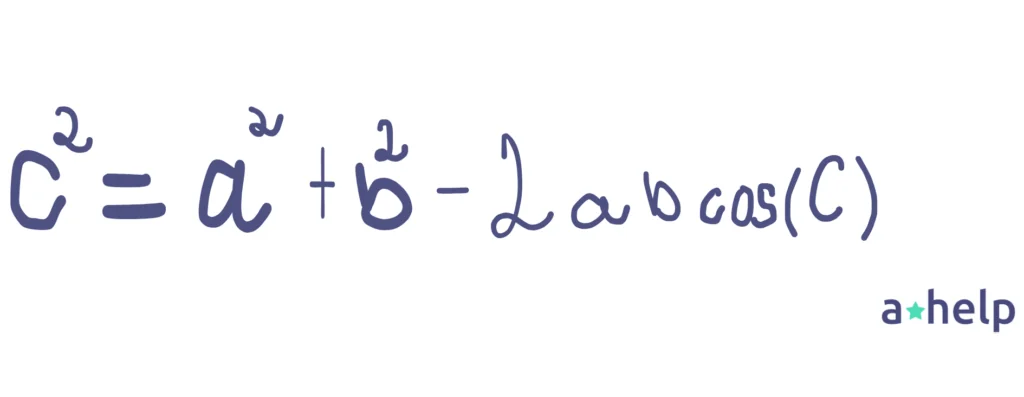
where a, b, and c are the sides, and C is the angle opposite side c.
When to use it: The Law of Cosines is perfect when you know:
- All three sides (SSS) – If you have all the sides, you can use this law to find any of the angles.
- Two sides and the included angle (SAS) – With two sides and the angle between them, you can find the missing side using this law.
By understanding these laws and knowing when to use them, you’ll be well-equipped to tackle any triangle problem, even if it’s not a right triangle.
Solving Math Problems
Let’s solve some problems to find the missing side lengths of triangles:
Example 1: Right Triangle
Problem:
Find the missing side length of a right triangle with one side measuring 3 cm and the hypotenuse measuring 5 cm.
Solution:
- Use the Pythagorean Theorem: a^2 + b^2 = c^2
- Plug in the known values: 3^2 + b^2 = 5^2
- Simplify: 9 + b^2 = 25
- Subtract 9 from both sides: b^2 = 16
- Take the square root: b-4 cm
Example 2: Equilateral Triangle
Problem:
Find the missing side length of an equilateral triangle with a perimeter of 18 cm.
Solution:
- Divide the perimeter by 3: 18 cm ÷ 3 = 6 cm.
- Each side of the equilateral triangle is 6 cm.
Example 3: Scalene Triangle using Law of Cosines
Problem:
Find the missing side length of a scalene triangle with sides of 7 cm and 9 cm and an included angle of 60°.
Solution:
- Use the Law of Cosines: c^2 = a^2 + b^2 – 2ab cos(C).
- Plug in the known values: c^2 = 7^2 + 9^2 – 2*(7)*(9)*cos(60°)
- Simplify: c^2 = 49+81−126*(0.5)
- Calculate: c^2 = 130−63=67
- Take the square root: c ≈ 8.2 cm.
Conclusion
Finding the missing side length of a triangle is a fundamental skill in geometry. By identifying the type of triangle and applying the appropriate mathematical formulas, such as the Pythagorean Theorem, Law of Sines, or Law of Cosines, you can solve these problems with confidence. Whether you’re working with right triangles, equilateral triangles, or scalene triangles, these tools will help you uncover the missing pieces of the puzzle.
FAQ
Follow us on Reddit for more insights and updates.




Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.