A polygon is a two-dimensional geometric figure that consists of a finite number of straight-line segments connected to form a closed shape. The line segments are called the sides or edges of the polygon, and the points where two sides meet are called the vertices or corners of the polygon. Polygons can be connected to other figures, such as a circle, for example. They can be either circumscribed or inscribed in the circles. We say a polygon is inscribed in a circle if all its vertices are points on this circle. So, imagine you have a circle and you draw a shape inside it so that all the corners of the shape touch the edge of the circle. This shape is what is called a polygon inscribed in a circle.

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
Properties of Polygons Inscribed in Circles
Before we dig into the specifics of the inscribed polygons, let’s be clear about what this word even means. “Inscribed” means that a shape (like a polygon) is drawn inside another shape (like a circle) so that all the corners of the inside shape touch the edge of the outside shape. We will also be using the word “circumscribed” a lot regarding the circles in our article. “Circumscribed” therefore means that a shape (like a circle in our case) is drawn around another shape (a polygon here).

As we figured that out we can move on to talking about the main properties of an Inscribed Polygon. One of the defining characteristics of these polygons is that all their vertices lie on the circumference of the circumscribing circle. This unique positioning leads to several more intricate aspects.
Firstly, all regular polygons, such as equilateral triangles, squares, and regular hexagons, can be perfectly inscribed in a circle. Their symmetrical nature allows each vertex to be equidistant (at the same distance) from the center of the circle. As a result
The center of the inscribed polygon is the same as the center of the circumscribing circle, and the radius of the polygon is equal to the radius of the circle.
The second important property involves the central angles and the internal angles of the polygon.
For any regular n-sided polygon inscribed in a circle, the central angle subtended by each side of the polygon is 360°/n.
Let’s look into this one more closely. Imagine you are drawing lines from the center of the circle to each corner of the shape. this way you’ll create angles with each of them being a slice of the whole circle. Since a circle has 360 degrees, and there are “n” sides (or corners) in the shape, each angle is 1/n of the whole circle, or 360°/n. So, if your shape has 4 sides (like a square), each angle would be 360°/4 = 90°.

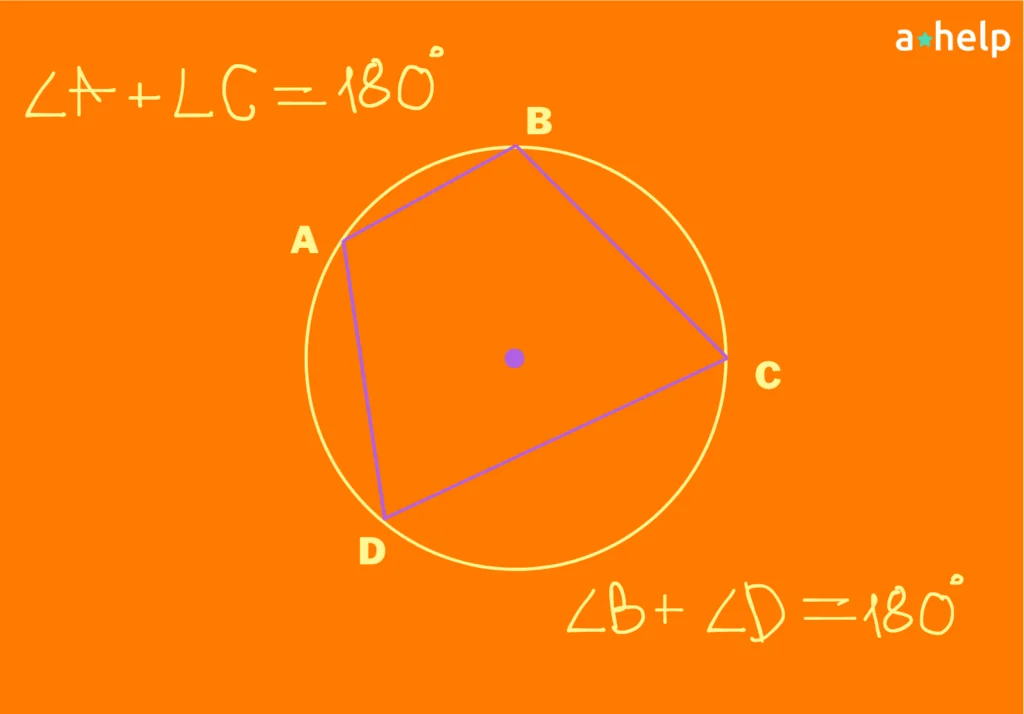
It’s also necessary to note here, that we can inscribe any type of polygon in a circle, and it doesn’t have to be a right one necessarily. In such cases, for example, if a quadrilateral is inscribed in a circle, then its opposite angles are supplementary (meaning they add up to 180 degrees).
We covered the angles, so the only logical step forward is to look into the sides of an inscribed polygon. A lot of times math problems ask you to find the length of the side of the given figure. To do that for an inscribed polygon, we can use the Law of Cosines. With its help, you can derive a general formula:
The length of a side (c) of a regular n-gon inscribed in a circle with radius r
c² = 2r² (1 – cos(360°/n)).
You should remember this formula, since it is widely used in solving problems related to inscribed polygons, such as determining the perimeter for example.
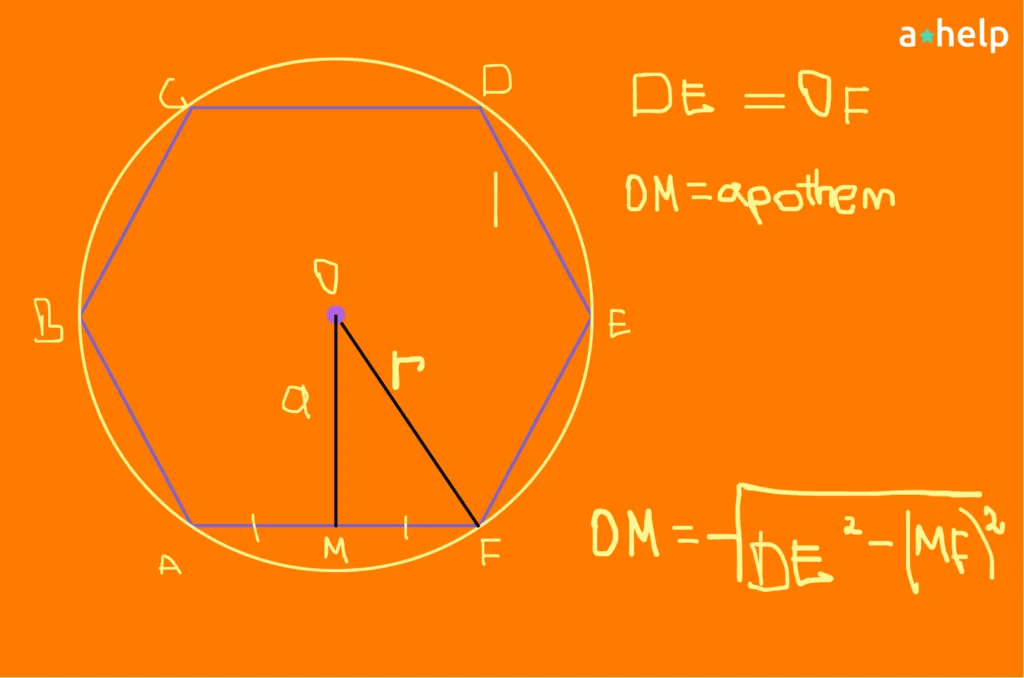
Looking at an Apothem of a Hexagon Inscribed in a Circle
The apothem is the distance between the center of the inscribed figure to the midpoint of one of its sides. Let’s use the example of a hexagon. When we look at a regular hexagon, where all sides are equal, each side has the same length as the radius of the circumscribing circle. This means if the radius is “r,” then the side length of the hexagon, “l,” is also “r.”
Now, imagine drawing a line from the center of the circle to the midpoint of one of the hexagon’s sides. This line is the apothem. To find its length, we can use a bit of Pythagoras’ theorem. We create a right-angled triangle by drawing the radius to one vertex of the hexagon and the apothem to the midpoint of the adjacent side. The base of this triangle is half the length of the hexagon’s side, or “r/2.” Applying Pythagoras’ theorem, we can calculate the length of the apothem.
Solving Math Problems with Inscribed Polygons
Example 1: Finding the Side Length of a Square Inscribed in a Circle
Problem: A square is inscribed in a circle with a radius of 6 cm. Find the length of a side of the square
Solution:
1. Draw a diagonal of the square, which will also be a diameter of the circle.
2. The length of the diagonal (d) is twice the radius of the circle, so d = 2 * 6 cm = 12 cm.
3. The diagonal of a square divides it into two right-angled triangles. In each triangle, the diagonal is the hypotenuse, and the sides of the square are the other two sides.
4. Using Pythagoras’ theorem, the side length (s) of the square can be calculated as: s² + s² = d² => 2s² = 12² => s² = 72 => s = √72 ≈ 8.49 cm.
Example 2: Calculating the Perimeter of a Hexagon Inscribed in a Circle
Problem: A regular hexagon is inscribed in a circle with a radius of 5 cm. Find the perimeter of the hexagon.
Solution:
1. In a regular hexagon inscribed in a circle, the side length (l) of the hexagon is equal to the radius of the circle, so l = 5 cm.
2. The perimeter (P) of the hexagon is the sum of the lengths of all its sides, so P = 6 * l = 6 * 5 cm = 30 cm.
Example 3: Finding the Area of a Pentagon Inscribed in a Circle
Problem: A regular pentagon is inscribed in a circle with a radius of 10 cm. Find the area of the pentagon.
Solution
1. The central angle of each segment of the pentagon is 360°/5 = 72°.
2. The apothem (a) of the pentagon can be found using the formula: a = r * cos(36°), where r is the radius of the circle. So, a = 10 * cos(36°) ≈ 8.09 cm.
3. The side length (l) of the pentagon can be found using the formula: l = 2 * r * sin(36°), so l = 2 * 10 * sin(36°) ≈ 11.76 cm.
4. The area (A) of the pentagon can be calculated using the formula: A = (1/2) * Perimeter * Apothem = (1/2) * 5 * 11.76 * 8.09 ≈ 237.60 cm².
FAQ
Follow us on Reddit for more insights and updates.




Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.