Tell us, who wasn’t confused at least on one geometry topic? It’s not like it’s the easiest class to exist. So no wonder that you would turn online (to this guide particularly) to try and answer the question of how to square a rectangle. So, let’s not waste our time whining about how hard math is, and finally find the answer to your question.
✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
A Guide to Squaring a Rectangle
First, let’s establish what ‘squaring a rectangle’ even means. Every square is a rectangle but not every rectangle is a square. We can only call a figure a square if it has four sides all of equal length, and four right angles (each of 90 degrees) So, to square a rectangle is to build a square that has the same area (equal area) as the one of a given rectangle. Basically, we use the dimensions that are given in a rectangle and apply them to construct a square.
Now, here’s what you have to do to square the given rectangle:
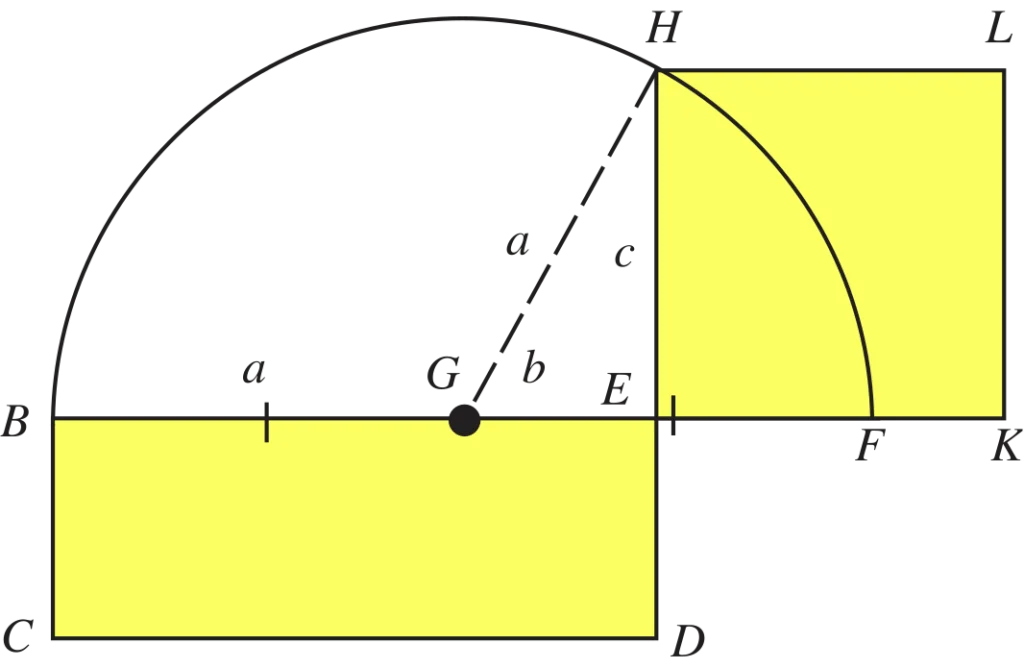
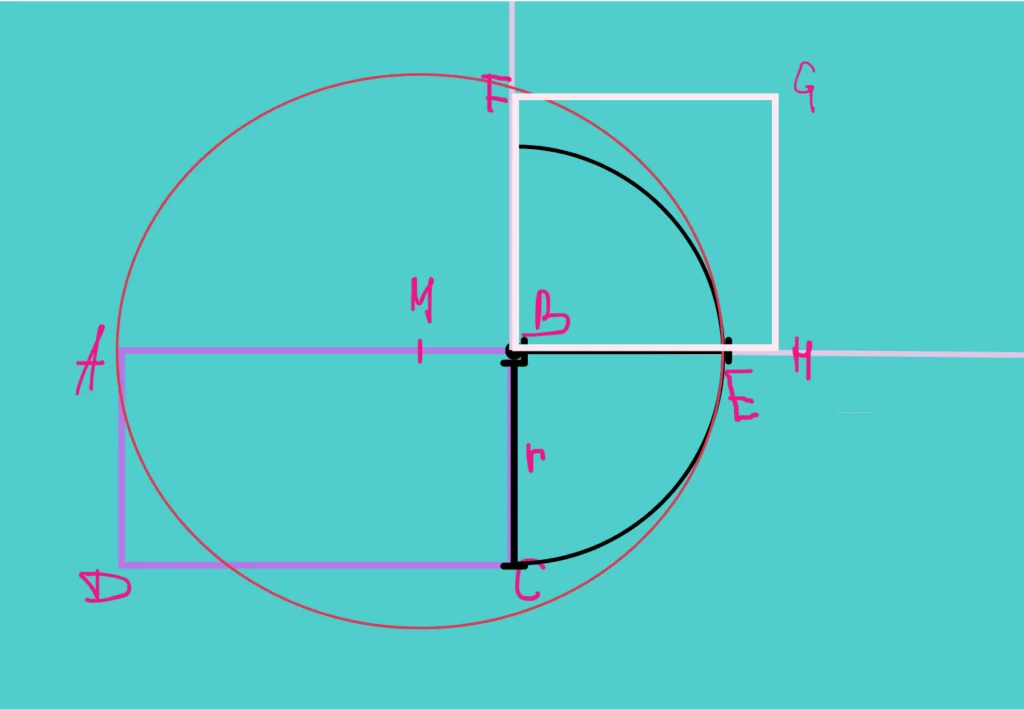
- Start with a rectangle. You can draw one on paper or use an existing rectangular object. Note the lengths of the longer side (length) and the shorter side (width). Let’s call our rectangle ABCD, with AB and CD as the longer sides, and BC and AD as the shorter sides.
- Then, draw a line beyond point B along AB.
- Using a compass, draw an arc centered at B with a radius BC (the shorter side of the rectangle). Mark the intersection of this arc with the extended line as point E.
- After that, locate the midpoint M of the segment AE and construct a circle centered at this point M with a radius equal to half of AE (ME and AM).
- Draw a line beyond point C along BC. Let F be the point where this line intersects the circle.
- After everything is done, you can use BF as the side length to construct your new square.
Here are a few pictures to help you visualize the building process:
Note that here, the naming of points is different from ours
Other Methods of Squaring a Rectangle
Squaring a rectangle might sound like an odd task at first, but in reality, it is a widely used concept, especially in construction works. Mostly, it is used specifically to make sure that the corners of the building are perfectly square, meaning they are all 90 degrees.
Construction workers though may not have all that time to draw everything like we did in the previous paragraph. That’s why they may use other methods to square a rectangle. For example a 3-4-5 technique. It’s a popular strategy that uses the Pythagorean theorem to make sure you build the right angles. By measuring 3 units on one side, 4 units on the adjacent side, and building the diagonal which equals 5 units, builders can create a perfect 90-degree angle. This method is scalable and can be adjusted for larger dimensions because here it’s not the numbers that matter but their correlation.
Another approach is the equal diagonal method, which involves measuring the diagonals of the proposed rectangle. If the diagonals are equal, the corners are therefore square. This method is simple and effective for structuring a correctly aligned foundation. Both techniques are necessary for achieving a perfectly square foundation, which is the basis for a sturdy and well-constructed building.
FAQ
Related
Follow us on Reddit for more insights and updates.
More from Geometry Guides
Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.