Understanding geometry can be a daunting task for many, presenting a significant shift from the straightforward nature of algebra to the more abstract and visual realm of geometry. This guide aims to demystify these concepts, making geometry more approachable and understandable through proper visualization techniques.

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
One of the most intriguing yet challenging aspects of geometry is the concept of proofs – logical arguments that demonstrate the truth of a geometric statement. Proofs are the backbone of mathematical reasoning, offering a window into the rigorous and logical structure that underpins the entire discipline of mathematics. However, mastering proofs, especially differentiating between lines and line segments, requires practice, a solid grasp of geometric principles, and an understanding of how to approach these problems systematically.
Geometry Proofs List
Geometry proofs form the core of mathematical reasoning within the discipline, illustrating the logical foundation underlying geometric concepts. Below is an overview of essential geometry proofs, each explained in straightforward terms, followed by a table summarizing these proofs and their explanations.
Parallel Lines
Parallel lines are two lines in the same plane that never meet, no matter how far they are extended. This concept is fundamental in understanding the properties of shapes and their angles.
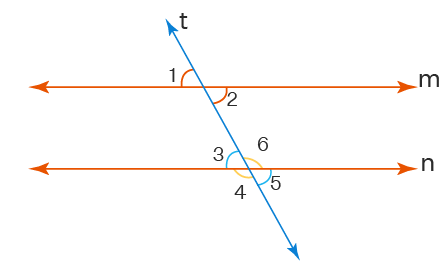
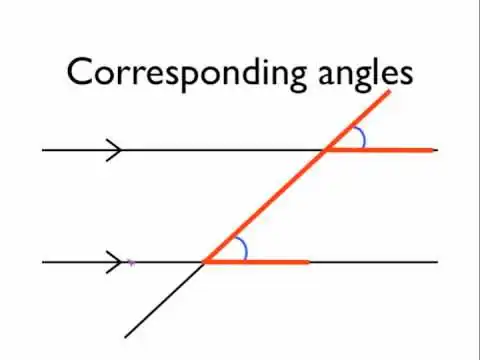
Corresponding Angles
When two parallel lines are intersected by a third line (known as a transversal), the angles in matching corners (corresponding angles) are equal. This proof is crucial for solving various geometric problems involving parallel lines and angles.
Vertical Angles
Vertical angles are formed when two lines intersect, creating two pairs of opposite angles that are equal. This concept is a key element in understanding the relationships between angles formed by intersecting lines.

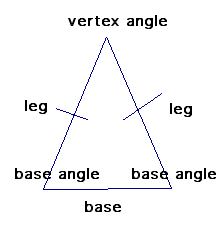
Isosceles Triangle Theorem
An isosceles triangle is defined by having at least two sides of equal length. This definition lays the groundwork for further exploration of triangles and their properties.
Building on the definition of an isosceles triangle, this theorem states that if a triangle is isosceles, then its base angles (the angles opposite the equal sides) are also equal. This theorem highlights the symmetrical properties of isosceles triangles.
| Proof | Explanation |
|---|---|
| Parallel Lines | Lines that do not intersect and are always equidistant. |
| Corresponding Angles | Angles that occupy the same relative position at each intersection where a straight line crosses two others. |
| Vertical Angles | Equal angles formed opposite each other when two lines intersect. |
| Isosceles Triangle | A triangle with at least two equal sides. |
| Isosceles Triangle Theorem | States that base angles in an isosceles triangle are equal. |
How to Solve Geometry Proofs?
Solving geometry proofs requires a systematic approach, combining logical reasoning with a deep understanding of geometric principles. Here’s how students can tackle geometry proofs effectively:
- 📖 Plan it out: Start by clearly defining the problem. Understanding precisely what is being asked is crucial for formulating a solution.
- 🔍 Identify known quantities: Look for given lengths, angles, and relationships within the problem. This information will serve as the foundation for building your proof.
- 📐 Utilize parallel lines: Recognize the role of parallel lines in your proof. The properties of parallel lines and their angles can simplify complex problems.
- ➡️ Apply if-then logic: Logical progression is key. Each step in your proof should follow logically from the previous one, leading to the conclusion.
- 🔄 Work backward if stuck: Sometimes, starting from the desired conclusion and working backward can reveal the necessary steps to arrive at the solution.
Wrap Up
With the right guidance, the intricate world of geometry and its proofs can be navigated with ease and confidence. Through a thorough understanding of essential geometry proofs and the application of systematic solving strategies, students can overcome their apprehensions and discover the logical beauty of geometry.
FAQ
Follow us on Reddit for more insights and updates.




Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.