A polygon is a two-dimensional geometric figure composed of a finite number of straight line segments connected end-to-end to form a closed loop. These segments are called edges or sides, and the points where two edges meet are the polygon’s vertices or corners. The word “polygon” comes from the Greek words “poly,” meaning “many,” and “gon,” meaning “angle.”

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
Polygons are a fundamental aspect of geometry, and they can be simple or complex, regular or irregular. They are characterized by the number of sides they have, which determines their shape and properties. Polygons can have as few as three sides, such as in a triangle, or as many as desired, with each additional side creating a new shape. The study of polygons is an essential part of understanding geometric principles and their applications in various fields, including art, architecture, and engineering.
Polygon Types, Shapes, and Number of Sides
Polygons are classified into various types based on their number of sides and their geometrical properties. The most common types are named for the number of sides they have. For example, a polygon with three sides is called a triangle, while one with four sides is known as a quadrilateral. As the number of sides increases, the names of the polygons become more complex, such as pentagon (five sides), hexagon (six sides), and so on. Here is a more detailed table chart showing the correlation between the number of sides of a polygon and their shape/name:
| Number of Sides | Name of Polygon | Characteristics |
|---|---|---|
| 3 | Triangle | Three angles, three vertices |
| 4 | Quadrilateral | Four angles, four vertices, includes squares, rectangles |
| 5 | Pentagon | Five angles, five vertices |
| 6 | Hexagon | Six angles, six vertices |
| 7 | Heptagon | Seven angles, seven vertices |
| 8 | Octagon | Eight angles, eight vertices |
| 9 | Nonagon | Nine angles, nine vertices |
| 10 | Decagon | Ten angles, ten vertices |
| 11 | Hendecagon | Eleven angles, eleven vertices |
| 12 | Dodecagon | Twelve angles, twelve vertices |
Each type of polygon has its own set of properties and formulas for calculating area, perimeter, and interior angles. Understanding these properties is crucial for solving geometric problems and for practical applications in design and construction.
Convex and Concave Polygons
A convex polygon is a type of polygon where all interior angles are less than 180°. This means that any line segment drawn between any two points on the boundary of the polygon will always lie entirely within the polygon. Convex polygons have no indentations or “inward” curves on their sides, resulting in a shape that appears to bulge outward. Examples of convex polygons include regular shapes like squares, rectangles, and regular hexagons, where all sides and angles are equal, as well as irregular shapes where the sides and angles may differ, but no interior angle exceeds 180°.
A concave polygon, in contrast, is a polygon that has at least one interior angle greater than 180°. This creates an indentation or “cave-in” effect on at least one side of the polygon, giving the appearance that part of the polygon is pushed inward. Concave polygons can have complex shapes, and they often resemble a convex polygon with a “bite” taken out of it. Star-shaped polygons, with their inward-pointing vertices, are classic examples of concave polygons.
Simple and Complex Polygons
A simple polygon is defined as a polygon that does not intersect itself. This means that its edges meet only at the vertices, and no two edges cross each other at any point other than these vertices. Simple polygons can be either convex or concave, but they maintain a single, unbroken boundary that encloses a single region of space. Most common polygons, such as triangles, rectangles, and pentagons, are simple polygons because they have a clear and straightforward shape without any self-intersecting lines.

On the other hand, a complex polygon, also known as a self-intersecting polygon, is a polygon whose sides cross over each other at one or more points that are not vertices. This crossing creates a shape that can be seen as a combination of multiple simple polygons, or as a single polygon with a more intricate boundary. Complex polygons often resemble a figure made up of several overlapping simple polygons. A typical example of a complex polygon is a five-pointed star, where the extensions of the sides intersect with each other, creating a shape that cannot be classified as a simple polygon.
How to Compute the Number of Sides of a Regular Polygon
In a regular polygon, all sides and angles are equal. To compute the number of sides (n) of a regular polygon, you can use the formula for the sum of interior angles:
Sum of interior angles=(n−2)×180∘
Rearranging the formula, you can find the number of sides:
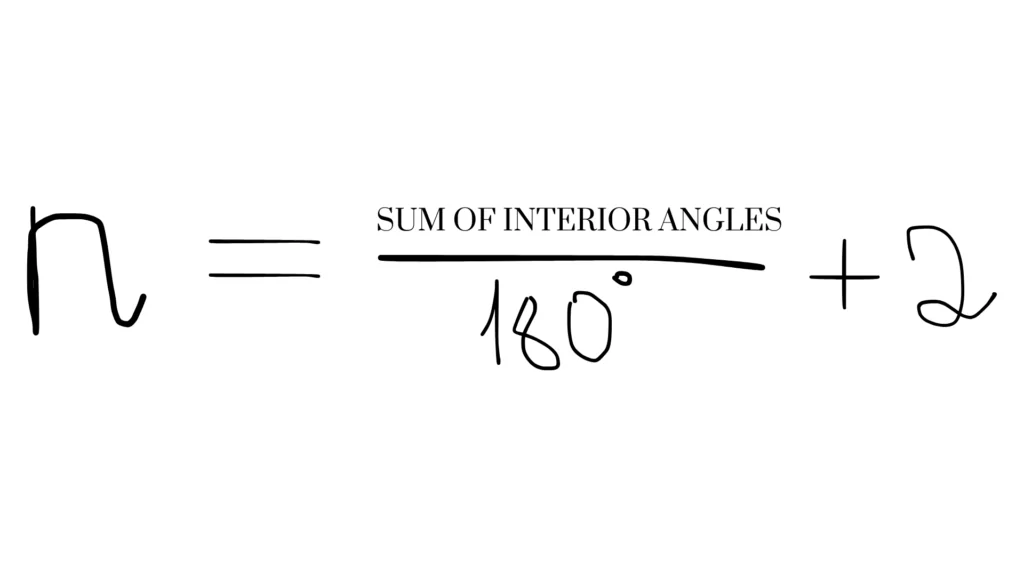
Using the formula of the sum of interior angles you cal also find the measure of each interior angle in a regular polygon by dividing this sum by the number of sides:
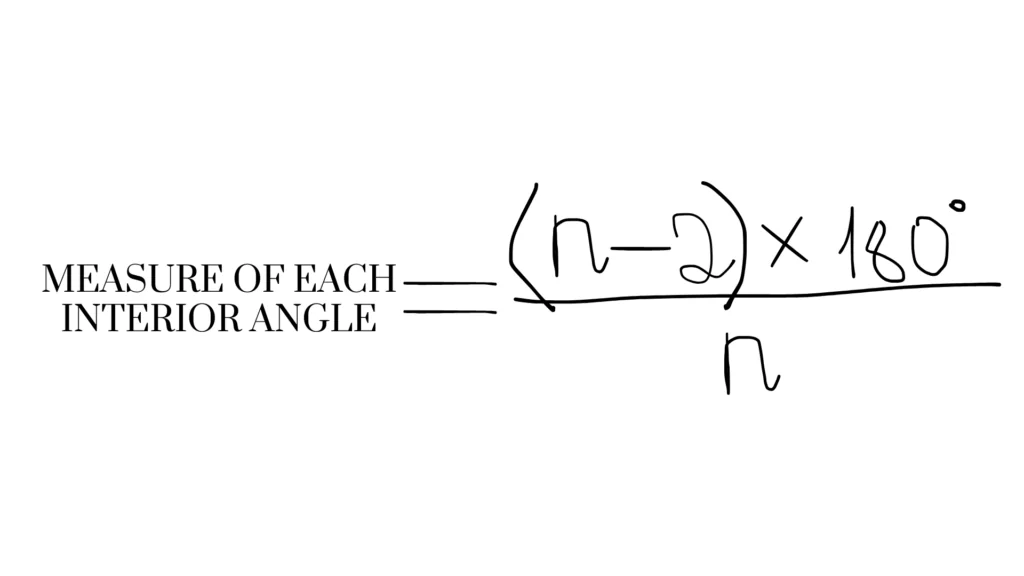
Conclusion
Polygons are fascinating geometric figures that come in various shapes and sizes, each defined by its number of sides. From simple triangles to complex star-shaped figures, polygons play a crucial role in geometry and our understanding of shapes. Whether it’s a regular polygon with equal sides and angles or a concave polygon that seems to cave inwards, each has its unique properties and formulas to explore. Understanding these concepts not only enriches our knowledge of geometry but also helps us appreciate the mathematical beauty in the world around
FAQ
Follow us on Reddit for more insights and updates.




Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.