Have you ever found yourself staring at a circular object, wondering just how long a string would need to be to wrap around it perfectly? If you’re a college student, you might have encountered this question in a geometry class or even while trying to figure out the size of a pizza. Understanding how to calculate the circumference of a circle is not only a fundamental concept in math but also a practical skill that can come in handy in real-life situations. So, let’s dive into the world of circles and unravel the mystery of their perimeters!

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
What’s Circumference
In geometry, the circumference is the distance around the edge of a circle. It’s akin to the perimeter of a polygon, but for a circle, which has a continuous curve.
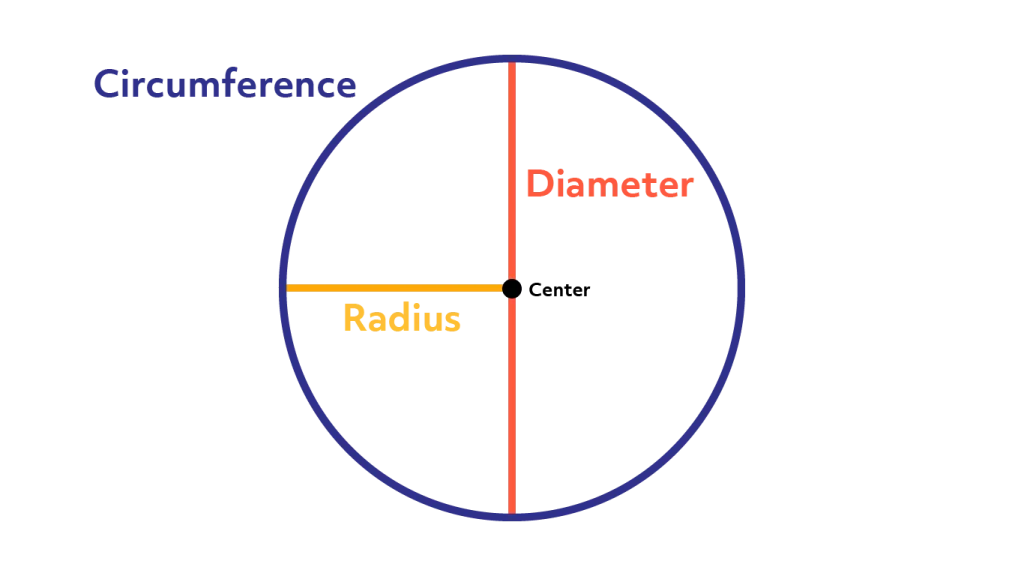
The formula to calculate the circumference is simple yet powerful: C = 2πr or C = πd. Here, C represents the circumference, r is the radius (the distance from the center of the circle to any point on its edge), and d is the diameter (the distance across the circle, passing through its center). The constant π (pi) is approximately equal to 3.14159, and it plays a crucial role in these formulas as it represents the ratio of the circumference of a circle to its diameter.
To use these formulas properly, you need to know either the radius or the diameter of the circle. Once you have one of these measurements, you can plug it into the formula and solve for the circumference. For instance, if you know the radius, you would use the formula C = 2πr; if you know the diameter, you would use C = πd.
Example Math Problem:
Imagine you’re working on a math problem where you need to find the circumference of a circular garden to determine how much fencing you’ll need to enclose it. The garden has a radius of 4 meters.
- Identify the given information: The radius of the garden is 4 meters.
- Choose the appropriate formula: Since you know the radius, use the formula C = 2πr.
- Substitute the value of the radius into the formula: Replace r with 4 meters, so the formula becomes C = 2π(4 m).
- Calculate the circumference: Use the approximate value of π (3.14159) to find the circumference: C = 2 * 3.14159 * 4 m ≈ 25.13 m.
- Interpret the result: The circumference of the garden is approximately 25.13 meters, so you would need about 25.13 meters of fencing to enclose the garden.
In this example, understanding how to calculate the circumference allowed you to solve a practical problem related to landscaping. Now you can see how important is geometry in our everyday lives. Having the power of mathematical formulas in your hands can easily help in solving real-world challenges.
Two Major Ways of Finding Circumference
Using the Radius
The most common method to calculate the circumference of a circle is by using its radius. The radius is the distance from the center of the circle to any point on its edge. The formula to find the circumference when you know the radius is straightforward: C = 2πr, where C is the circumference and r is the radius of the circle.
Example:
Suppose you have a circle with a radius of 5 cm. To find its circumference, follow these steps:
- Identify the radius: The radius is given as 5 cm.
- Apply the formula: Use the formula C = 2πr.
- Substitute the value of the radius: Replace r with 5 cm in the formula, so it becomes C = 2π(5 cm).
- Calculate: Use the approximate value of π (3.14159) to find the circumference: C = 2 * 3.14159 * 5 cm ≈ 31.42 cm.
- Conclusion: So, the circumference of the circle is approximately 31.42 cm.
Using the Diameter
If you know the diameter of the circle, you can also find its circumference using the formula C = πd. The diameter is twice the length of the radius and is the distance across the circle through its center. This method is particularly useful when the diameter is more readily available than the radius.
Example:
Imagine a circular table with a diameter of 1 meter. To calculate its circumference, follow these steps:
- Identify the diameter: The diameter is given as 1 meter.
- Apply the formula: Use the formula C = πd.
- Substitute the value of the diameter: Replace d with 1 meter in the formula, so it becomes C = π(1 m).
- Calculate: Use the approximate value of π (3.14159) to find the circumference: C = 3.14159 * 1 m ≈ 3.14 m.
- Conclusion: Therefore, the circumference of the table is approximately 3.14 meters.
In both methods, the key is to identify the given measurement (radius or diameter) and then apply the corresponding formula to calculate the circumference. With practice, these calculations become straightforward and quick to perform.
Conclusion
Calculating the circumference of a circle is a fundamental skill in geometry that has practical applications in everyday life. Whether you’re using the radius or the diameter, the key is to understand and apply the formulas correctly. With a bit of practice, you’ll be able to quickly and accurately find the circumference of any circle, making you a whiz at geometry and a handy person to have around when pizza is involved! So, next time you’re faced with a circular challenge, remember the tips and formulas from this article, and you’ll have the answer in no time.
FAQ
Follow us on Reddit for more insights and updates.




Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.