Composite shapes are figures made up of two or more simple shapes, such as rectangles, triangles, or circles. Imagine putting together pieces of a puzzle; each piece is a simple shape, but when combined, they form a composite shape.

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
Knowing how to find the area of these shapes is important in various fields, like in construction, when it helps in determining the amount of material needed for a project. Or maybe in design, when you need to create a highly precise layout. Knowing how to calculate the area of composite shapes is easy; it just needs a little bit of practice.
What Are Composite Shapes?
Composite shapes are figures made by combining two or more simple shapes, such as rectangles, circles, triangles, or squares. Think of them like a patchwork quilt: each patch is a simple shape, and when sewn together, they form a more complex shape.
Here are some examples of common composite shapes you’ve surely seen in your everyday life:
- A house shape. This is a composite shape made by combining a rectangle (for the main part of the house) with a triangle (for the roof).
- A T-shape. This shape is formed by joining two rectangles together, one positioned horizontally on top of the other, which is vertical.
- A keyhole. This shape is created by combining a circle (for the round part of the keyhole) with a narrow rectangle (for the key slot).
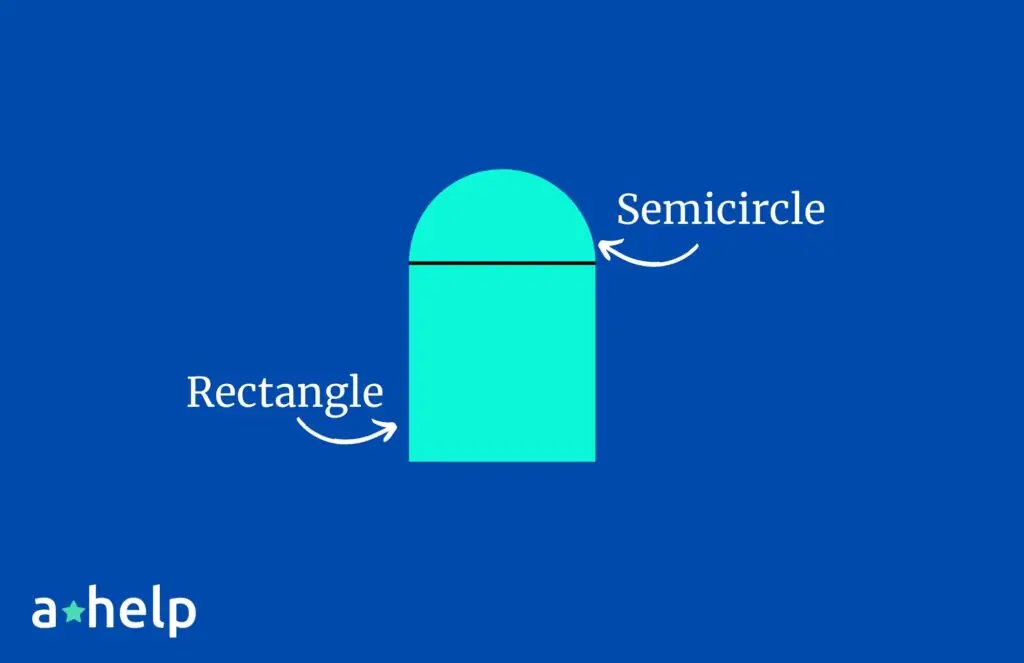
- A window with a semicircular arch. Here, a rectangle (for the main part of the window) is combined with a semicircle (for the arch at the top).

How to Break Composite Shapes Into Simpler Shapes
To find the area of a composite shape, we first need to break it down into simpler shapes that we can easily work with. This process is basically dividing the shape into smaller, more manageable pieces.
Let’s say you have a composite shape made of a rectangle and a triangle. You would start by identifying these two simpler shapes within the larger figure. Once you’ve done that, you can focus on each shape individually.
For the rectangle, you would measure its length and width, and for the triangle, you would find its base and height. With these measurements, you can calculate the area of each simple shape using the formulas you already know: area of a rectangle is length times width, and area of a triangle is half the base times the height.
By breaking down the composite shape into simpler shapes, you make the problem of finding the total area much easier to solve. After finding the area of each simple shape, you can add them together to get the total area of the composite shape.
Step-by-Step Guide to Finding the Area
Finding the area of a composite shape can be done in a few simple steps.
Step 1: Identify the shapes.
First, look at the composite shape and identify the simpler shapes that make it up. These could be rectangles, triangles, circles, or other familiar shapes. Here, the shapes are a rectangle and a semicircle.
Step 2: Find the area of each shape.
Use the formulas you know for each shape, like length times width for a rectangle or base times height divided by two for a triangle. For the rectangle, if the length is 10 units and the width is 5 units, the area is 50 square units. For the semicircle, if the diameter is 5 units, the radius is 2.5 units, and the area is 1/2 * π * (2.5)^2 ≈ 9.82 square units.
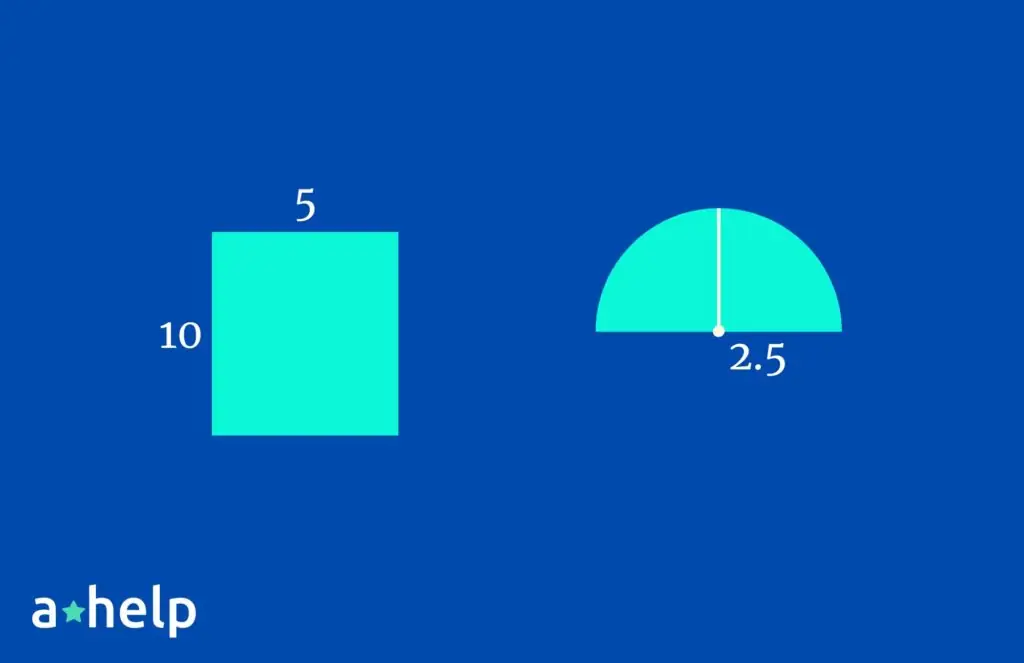
Step 3: Add or subtract the areas of the simple shapes as appropriate.
Then, depending on how the shapes are put together, you might need to add or subtract their areas. If the shapes are all next to each other, add their areas. If one shape is inside another, subtract the area of the smaller shape from the larger one.
Here, since the semicircle is a cutout, subtract its area from the rectangle’s area.
Step 4: Calculate the total area of the composite shape.
Finally, add up all the areas you’ve calculated to get the total area of the composite shape. This total is the amount of space that the composite shape covers. In our task, the total area of the composite shape is 50 – 9.82 = 40.18 square inches. Yay, you have your answer!
If you feel like you need a little more practice, you will find two exercises below to really dive deeper into the topic.
FAQ
Follow us on Reddit for more insights and updates.




Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.