How to Prove a Rectangle

Geometry is not just about shapes; it’s about the stories they tell and the mysteries they hold. One of the most familiar yet intriguing shapes is the rectangle. Students often encounter the challenge of proving that a given quadrilateral is a rectangle. This article will guide you through the fascinating journey of proving a rectangle, unveiling the secrets behind its right angles and equal sides.

What is a Quadrilateral?

In geometry, a quadrilateral stands out as a fundamental shape, defined as a polygon with exactly four sides and four angles. This definition may seem simple, but within it lies a diverse family of shapes, each with its own distinctive features and properties. Quadrilaterals are a cornerstone of geometric studies, offering a rich field for exploration and analysis.

The family of quadrilaterals is vast and varied, including well-known members like squares, rectangles, trapezoids, rhombuses, and parallelograms. Each of these shapes adheres to the basic definition of a quadrilateral but brings its own set of rules regarding side lengths, angle measurements, and symmetry.

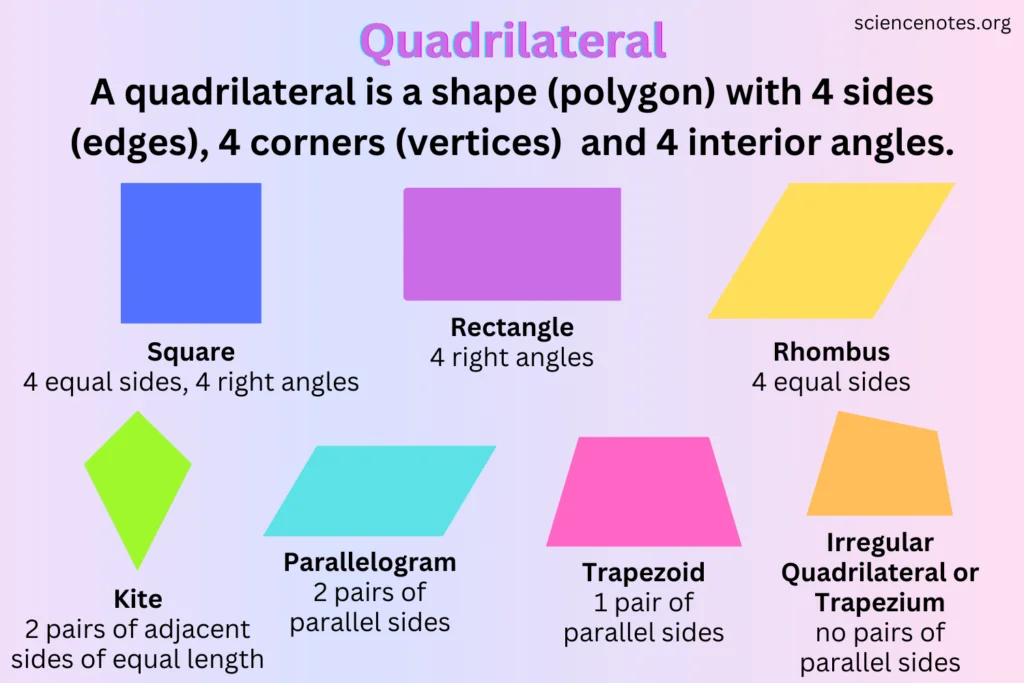
One of the defining characteristics of quadrilaterals is their ability to be classified based on their properties. For instance, a square is a quadrilateral with four equal sides and four right angles, while a rectangle has four right angles but only opposite sides are equal. A parallelogram, on the other hand, has opposite sides that are parallel and equal in length but do not necessarily have right angles.

The interior angles of a quadrilateral are another important feature. Regardless of the specific type of quadrilateral, the sum of its interior angles always adds up to 360°. This property is crucial for solving various geometric problems and is a fundamental theorem in the study of polygons. Quadrilaterals can also be distinguished by their symmetry. Some, like squares and rectangles, have lines of symmetry and rotational symmetry, making them highly regular shapes. Others, like trapezoids, may lack symmetry, giving them a more irregular appearance.

Characteristic	Description
Four Sides	A quadrilateral has exactly four sides.
Four Angles	It also has four angles, with their sum always equal to 360°.
Interior Angles	The angles inside a quadrilateral add up to 360°.
Types	Squares, rectangles, trapezoids, and parallelograms The type is based on their side lengths and angle measurements.

Proving that a Quadrilateral Is a Rectangle

To prove that a quadrilateral is a rectangle, we need to establish that it satisfies the definition of a rectangle: a quadrilateral with four right angles. There are several methods to demonstrate this:

1. Show All Angles Are Right Angles:
   • Approach: Measure or calculate the angles of the quadrilateral. If each angle measures 90°, the quadrilateral is a rectangle.
     
   • Application: This method is often used when you have access to the angle measurements, either through geometric constructions or given information in a problem.
     
2. Prove It’s a Parallelogram with One Right Angle:
   • Approach: First, show that the quadrilateral is a parallelogram by proving that opposite sides are parallel (e.g., using slope in a coordinate plane or showing alternate interior angles are equal). Then, demonstrate that one of the angles is a right angle.
     
   • Application: This method is useful when you can easily prove the quadrilateral is a parallelogram (e.g., if it’s given or if you have coordinates) and you have information about one of the angles.
     
3. Use Diagonals:
   • Approach: Prove that the diagonals of the quadrilateral are congruent (e.g., by using the distance formula in a coordinate plane or congruent triangles). If the quadrilateral is already proven or given to be a parallelogram, and its diagonals are congruent, then it must be a rectangle.
     
   • Application: This method is particularly effective when working with coordinate geometry or when you can establish congruence between triangles formed by the diagonals.

Each of these methods relies on different properties of rectangles and parallelograms, allowing for flexibility in how you approach a proof. Depending on the information provided and the context of the problem, one method may be more suitable than another. In all cases, it’s essential to provide clear and logical reasoning to support your conclusion that the quadrilateral is indeed a rectangle. We’ve searched the Internet a bit and found the following video that can clarify anything that is left unclear after our explanation.

Proving a Rectangle: Math Problem Examples

Let’s explore three examples of how to prove a quadrilateral is a rectangle:

Example 1: Using Angle Measures

Problem:
Prove that a quadrilateral with vertices A(2,3), B(6,3), C(6,7), and D(2,7) is a rectangle.

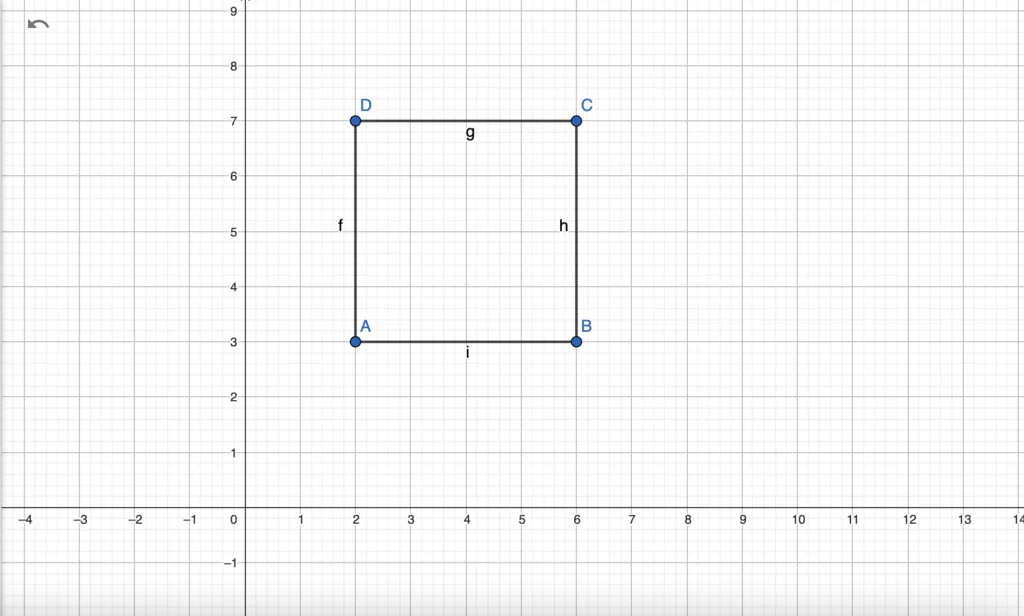
Solution:

1. Calculate Slopes: Find the slopes of the sides to determine if they are parallel.
   • AB and CD are horizontal lines (y-coordinates are the same), so their slopes are 0.
   • BC and AD are vertical lines (x-coordinates are the same), so their slopes are undefined.
2. Check for Right Angles: Since AB is horizontal and AD is vertical, the angle between them is a right angle. Similarly, all other angles are right angles.
3. Conclusion: Since all angles are right angles and opposite sides are parallel, the quadrilateral ABCD is a rectangle.

Example 2: Using Parallelogram Properties and One Right Angle

Problem:
Prove that a quadrilateral with vertices A(1,1), B(4,4), C(7,1), and D(4,-2) is a rectangle.

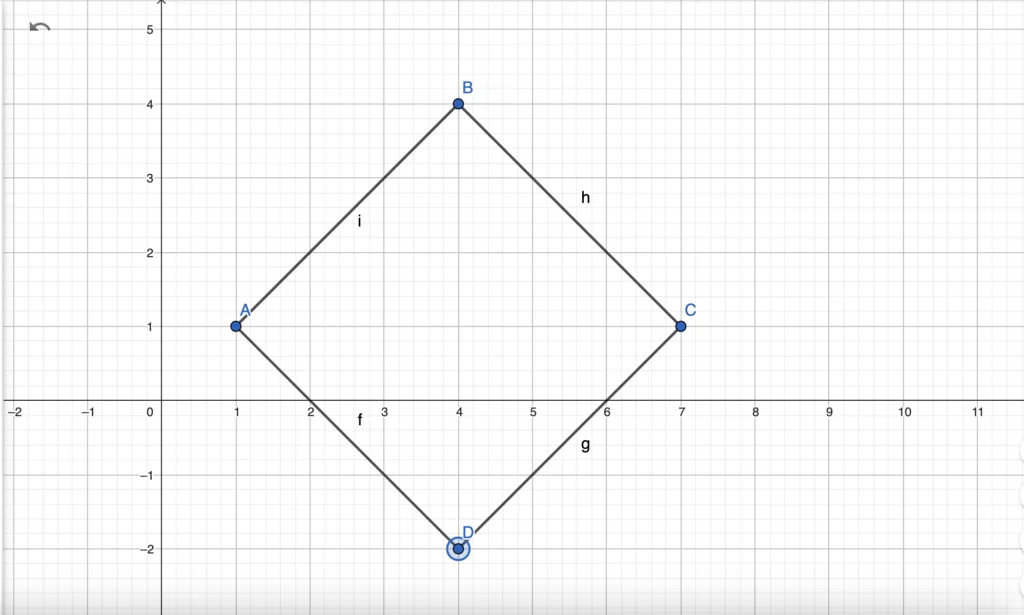
Solution:

1. Show It’s a Parallelogram: Prove that opposite sides are parallel by showing their slopes are equal.
   • Slope of AB = (4-1)/(4-1) = 1
   • Slope of CD = (1-(-2))/(7-4) = 1
   • Slope of BC = (4-1)/(4-7) = -1
   • Slope of AD = (1-(-2))/(1-4) = -1
2. Identify a Right Angle: The slopes of AB and AD are negative reciprocals, indicating that angle BAD is a right angle.
3. Conclusion: Since the quadrilateral is a parallelogram with one right angle, it is a rectangle.

Example 3: Using Congruent Diagonals

Problem:
Prove that a quadrilateral with vertices A(0,0), B(5,0), C(5,3), and D(0,3) is a rectangle.

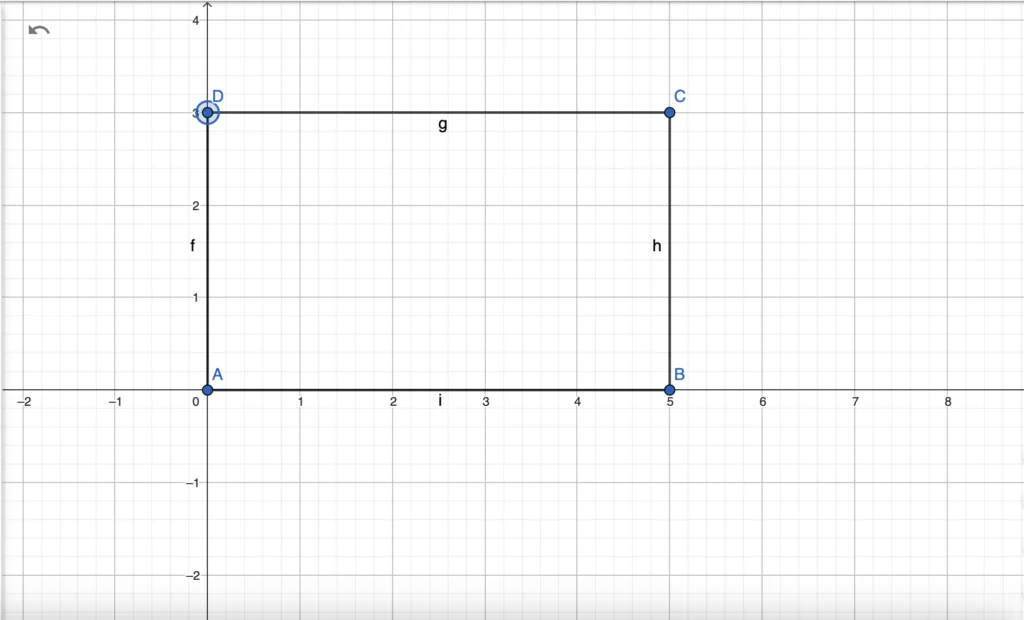
Solution:

1. Calculate Diagonal Lengths: Use the distance formula to find the lengths of the diagonals AC and BD.
   • Length of AC = √[(5-0)² + (3-0)²] = √(25 + 9) = √34
   • Length of BD = √[(5-0)² + (3-0)²] = √(25 + 9) = √34
2. Check for Parallelogram: Show that opposite sides are parallel (same slope).
   • Slopes of AB and CD are 0 (horizontal lines).
   • Slopes of BC and AD are undefined (vertical lines).
3. Conclusion: Since the diagonals are congruent and the quadrilateral is a parallelogram, it is a rectangle.

Conclusion

Proving a quadrilateral is a rectangle may seem daunting at first, but with a clear understanding of the properties of rectangles and a step-by-step approach, it becomes an achievable task. By focusing on right angles, parallelogram properties, and diagonal congruence, you can confidently prove the rectangular nature of a quadrilateral. So, the next time you’re faced with this challenge, remember these strategies and tackle the problem with ease.

FAQ

Related

A*Help Insights - sign up for our Newsletter

Sign up

Thanks for signing up!

Something went wrong. Please try again later.

Follow us on Reddit for more insights and updates.