How to Prove Triangles Similar – Quick Guide

In geometry, triangles are fascinating shapes that come with a set of intriguing properties. One such property is similarity, which allows us to compare triangles based on their shapes, regardless of their sizes. Proving triangles similarly is a fundamental skill in geometry that has practical applications in various fields, including engineering, architecture, and even art.

 

What Does Similarity Mean in Geometry?

Similarity is like a secret code that tells us when two figures are essentially the same shape, even if they’re not the same size. It’s like looking at two photos of the same object, one zoomed in and one zoomed out. They’re the same thing, just at different scales.

When we talk about similar triangles, we’re saying that they’re like geometric twins. Their corresponding angles match up perfectly, so they have the same “face,” so to speak. But it’s not just about the angles. The sides of these triangles are in proportion, which means if you were to measure them, you’d find that the lengths are scaled versions of each other. It’s like one triangle is a mini-me or a giant version of the other.

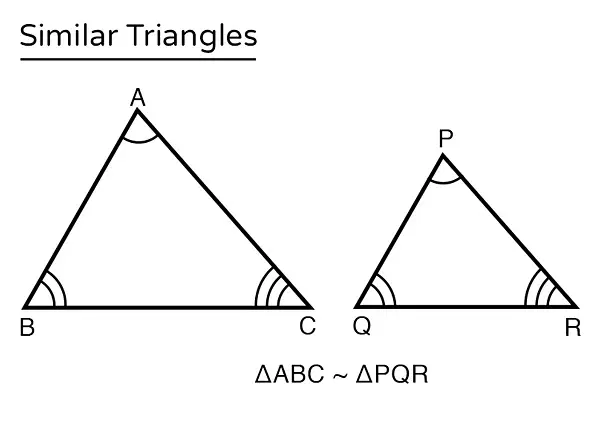
Imagine you have two triangles, and you can magically stretch or shrink one without changing its shape. If you can make it match the other triangle exactly, then they’re similar. This concept of similarity is super useful because it lets us compare shapes, solve problems, and understand the world around us in a more mathematical way. So, next time you see two shapes that look alike but are different sizes, remember, they might just be similar!

What Are the Triangle Similarity Criteria?

Proving that triangles are similar is like solving a puzzle. We use specific criteria, or “clues,” to figure out if two triangles are basically the same shape. These criteria are all about how the angles and sides of the triangles relate to each other. Let’s dive into the three main criteria for triangle similarity:

1. Angle-Angle (AA) Similarity: This criterion is all about the angles. If two angles in one triangle are exactly the same as two angles in another triangle, then the triangles are considered similar. It’s like if two people have the same eye color and smile – you can tell they’re related! In geometry, if two triangles share two congruent angles, the third angle must be congruent too, since the angles in a triangle always add up to 180 degrees. So, by knowing just two angles are the same, we can say the whole triangle is similar.
2. Side-Side-Side (SSS) Similarity: This one is about the sides. If the lengths of the corresponding sides of two triangles are in the same proportion, then the triangles are similar. For example, if one triangle has sides that are twice as long as the sides of another triangle, they’re similar. It’s like comparing two photographs of the same object taken from different distances – they show the same thing, just at different scales.
3. Side-Angle-Side (SAS) Similarity: This criterion combines sides and angles. If two sides of one triangle are in the same proportion as two sides of another triangle, and the angles between those sides are equal, then the triangles are similar. It’s like saying if two people have the same height-to-weight ratio and the same nose shape, they have a similar appearance.

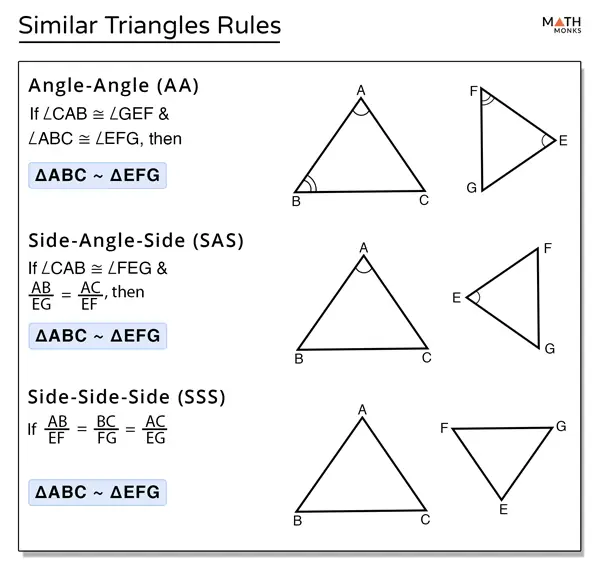
Three Accepted Methods for Proving Triangles Similar

Based on these three criteria for triangles similarity, there are therefore 3 methods to prove such similarity.

AA Similarity

Show that two angles of one triangle are congruent to two angles of another triangle. Since the sum of the angles in a triangle is always 180 degrees, if two angles are congruent, the third angle must also be congruent, proving the triangles are similar.

Problem:
Prove that triangles ABC and DEF are similar given that ∠A = 50°, ∠B = 60°, ∠D = 50°, and ∠E = 60°.

Solution:

1. We know that the sum of the angles in a triangle is 180°.
2. In triangle ABC, ∠C = 180° – (∠A + ∠B) = 180° – (50° + 60°) = 70°.
3. In triangle DEF, ∠F = 180° – (∠D + ∠E) = 180° – (50° + 60°) = 70°.
4. We have ∠A = ∠D and ∠B = ∠E. Since the third angles ∠C and ∠F are also equal, the triangles are similar by AA similarity (AAA is a special case of AA).

SSS Similarity

Demonstrate that the ratios of the corresponding sides of two triangles are equal. This can be done by dividing the lengths of corresponding sides and showing that the ratios are the same for all three pairs of sides.

Problem:
Determine if triangles GHI and JKL are similar given that GH = 4 cm, HI = 6 cm, IJ = 8 cm, JK = 6 cm, KL = 9 cm, and LJ = 12 cm.

Solution:

1. Calculate the ratios of the corresponding sides:
   • GH/JK = 4 cm / 6 cm = 2/3
   • HI/KL = 6 cm / 9 cm = 2/3
   • IJ/LJ = 8 cm / 12 cm = 2/3
2. All the ratios of the corresponding sides are equal (2/3).
3. Therefore, triangles GHI and JKL are similar by SSS similarity.

SAS Similarity

Prove that two sides of one triangle are proportional to two sides of another triangle and that the angles between these sides are congruent. This method combines the properties of proportional sides and congruent angles to establish similarity.

Problem:
Prove that triangles MNO and PQR are similar given that MN/PQ = 3/4, NO/QR = 3/4, and ∠N = ∠Q.

Solution:

1. We are given that the ratios of two pairs of corresponding sides are equal: MN/PQ = NO/QR = 3/4.
2. We are also given that the included angles are congruent: ∠N = ∠Q.
3. Therefore, triangles MNO and PQR are similar by SAS similarity.

Finding Missing Side Lengths in Similar Triangles

Once you’ve established that two triangles are similar, you unlock a powerful tool for finding missing side lengths: the concept of proportional sides. Similar triangles maintain the same shape, which means their corresponding sides are proportional. This proportionality is governed by a scale factor, which we’ll call k.

Let’s say you have two similar triangles, Triangle 1 and Triangle 2. The scale factor k describes how much larger or smaller Triangle 2 is compared to Triangle 1. Mathematically, this relationship is expressed as:

or, equivalently,

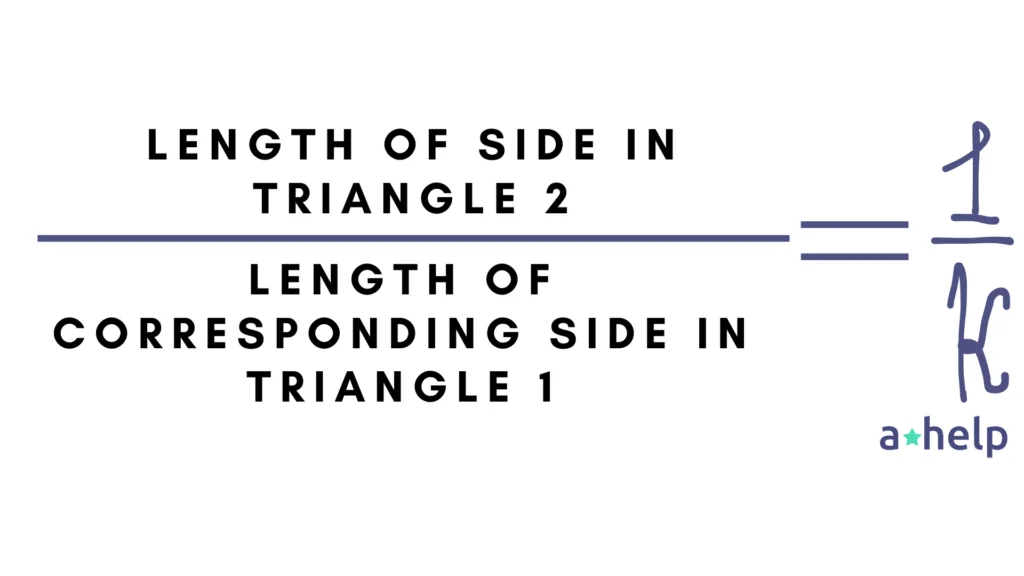
This equation tells us that if you multiply the length of a side in Triangle 1 by �k, you’ll get the length of the corresponding side in Triangle 2, and vice versa. Now, imagine you know the lengths of some sides but there’s one side length missing. You can set up a proportion using the known side lengths and the scale factor to find the unknown length. Here’s how you do it:

• Set up the proportion: Write an equation that relates the known side lengths and the unknown length using the concept of proportional sides.
• Cross-multiply: Multiply the terms diagonally across the equal sign. This will give you an equation where the unknown length is multiplied by a known number.
• Solve for the unknown: Use algebraic manipulation to isolate the unknown length on one side of the equation. This might involve dividing both sides of the equation by a number or subtracting a number from both sides.
• Check your work: Once you’ve found the missing length, double-check your calculations to make sure everything adds up.

By following these steps and using the principle of proportional sides, you can confidently find missing side lengths in similar triangles, unlocking a world of geometric possibilities!

Conclusion

Proving triangles similar is a crucial aspect of geometry that allows us to understand the relationships between different shapes. By mastering the triangle similarity criteria and learning how to apply them, you can unlock a world of geometric possibilities. Whether you’re solving complex problems or simply exploring the beauty of shapes, the ability to prove triangles similar is an invaluable tool in your mathematical toolkit.

FAQ

Related

A*Help Insights - sign up for our Newsletter

Sign up

Thanks for signing up!

Something went wrong. Please try again later.

Follow us on Reddit for more insights and updates.