Is a Kite a Parallelogram

The world of geometry is filled with various shapes, each with its unique properties and characteristics. Among these shapes, kites, and parallelograms are two quadrilaterals that often confuse students. Today, we’re going to dive into the world of kites, check out the different types of kites, and answer the main question: Is a kite a parallelogram?

What Are the Properties of a Kite?

Picture a kite flying high in the sky – it has a special shape, right? In geometry, a kite is a four-sided figure, or quadrilateral, with some cool features:

1. Two Pairs of Adjacent Congruent Sides: Imagine drawing a kite on paper. You’ll notice that it has two pairs of sides that are the same length, and these equal sides are right next to each other, not across from each other like in a parallelogram. So, if the kite’s sides are a, a, b, and b, the sides that are the same length (a and a, b and b) are touching.
2. One Pair of Opposite Angles Are Equal: If you look at the angles inside the kite, you’ll find that two opposite angles are the same size. These are the angles formed by the sides that are not equal.
3. Perpendicular Diagonals: A kite has two diagonals, which are lines that connect opposite corners. In a kite, these diagonals meet at a right angle or 90 degrees. This means they form a perfect “L” shape where they cross.
4. Bisected Diagonals: Not only do the diagonals of a kite cross at a right angle, but one of the diagonals also cuts the other one in half. This means that the longer diagonal is divided into two equal parts by the shorter diagonal.
5. Area Formula: The area of a kite can be found using the formula: Area = (Diagonal 1 × Diagonal 2) / 2. So, if you know the lengths of the diagonals, you can easily calculate the kite’s area.
6. Symmetry: A kite has one line of symmetry, which is the line that runs along the longer diagonal. This means if you fold the kite along this line, the two halves will match up perfectly.

What Is the Shape of a Kite?

When you think of a kite, you might imagine the classic toy flying in the sky, but in geometry, a kite can take on various shapes, each with its own charm. The key feature that all kites share is having two pairs of adjacent sides that are equal in length. This means the sides that are next to each other are the same length, but the lengths can vary between the pairs.

Now, let’s talk about the two main groups of kite shapes: convex kites and concave kites.

• Convex Kites: These are the kites that most people picture. All the interior angles in a convex kite are less than 180°, which means they don’t curve inward. Convex kites are symmetrical, meaning if you draw a line down the middle (along the longer diagonal), the two halves of the kite will be mirror images of each other. This symmetry creates two isosceles triangles, which are triangles with two sides of equal length. The longer diagonal of a convex kite acts as the line of symmetry and the base of these isosceles triangles.

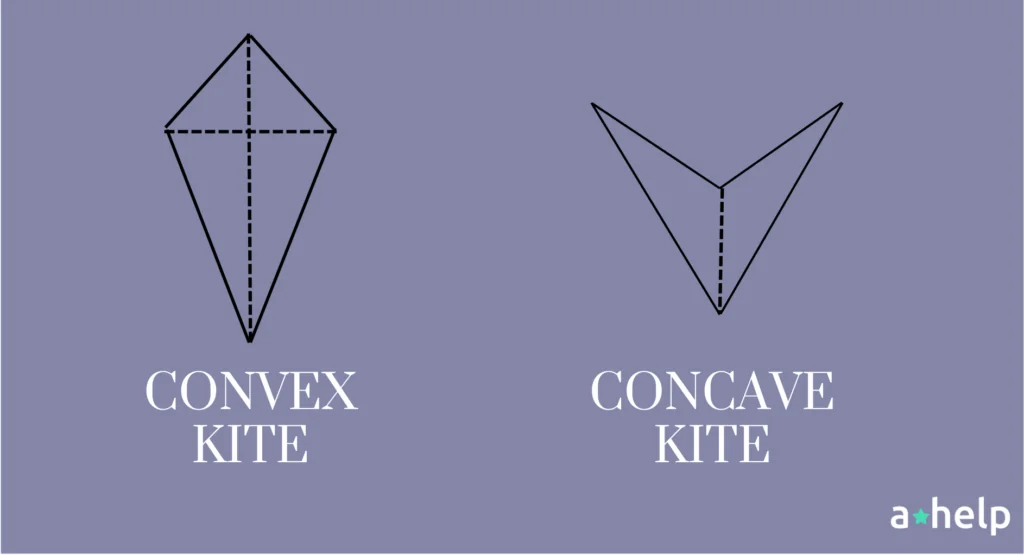
• Concave Kites: Also known as darts or arrowheads, concave kites have a bit of a twist. One of their interior angles is greater than 180°, which gives them a sort of indented or “caved-in” appearance on one side. Unlike convex kites, concave kites are not symmetrical. They resemble an arrow or a dart, with a pointed end and a wider base. The longer diagonal in a concave kite still bisects the kite, but it does not create symmetrical halves.

While all kites share the fundamental property of having two pairs of adjacent equal sides, the variety in their shapes comes from the differences in their angles. Convex kites are symmetrical with all angles less than 180°, forming isosceles triangles, while concave kites have one angle greater than 180°, giving them an arrow-like shape. Understanding these differences can help you identify and classify kites in geometry with ease!

A Kite is a Parallelogram Only When it is a Rhombus

Let’s talk about when a kite can transform into a parallelogram! You see, a parallelogram is a shape with opposite sides that are both equal in length and parallel to each other. Now, a kite usually doesn’t fit this description because, although it has two pairs of sides that are the same length, these sides are next to each other, not opposite. Plus, the sides of a kite don’t run parallel to each other like train tracks, which is a must-have feature for a parallelogram.

But here’s where it gets interesting: there’s a special kind of kite called a rhombus. A rhombus is like a superhero version of a kite because all four of its sides are equal in length. This is where the magic happens – because all the sides are the same, the opposite sides end up being equal and parallel, just like in a parallelogram. So, in this special case, our kite becomes a parallelogram!

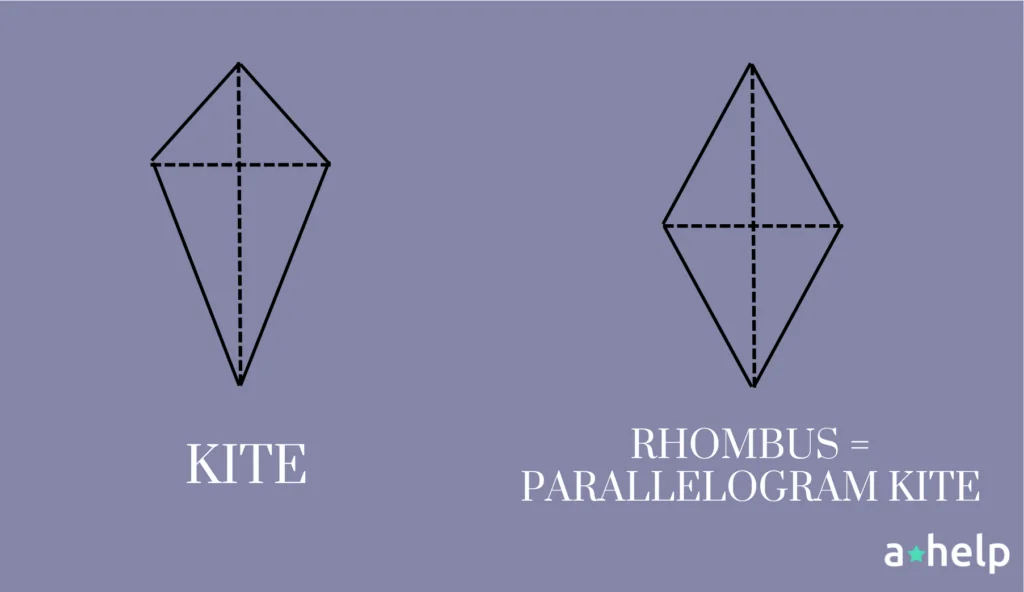
To sum it up, think of a kite as a regular person and a parallelogram as a superhero. Most kites are just regular folks, with sides that are equal but not parallel. But when a kite becomes a rhombus, it’s like it’s gained superpowers, with all sides equal and opposite sides parallel, turning it into a superhero parallelogram!

Properties of Diagonals of a Kite

The diagonals—those straight lines connecting opposite corners—play a starring role with their unique properties.

1. Equal Adjacent Sides: Kites have four sides, with two pairs of adjacent (next to each other) sides being equal in length. This means that the sides that touch each other are the same length, forming a symmetrical shape.
2. Diagonals: Kites have two diagonals that intersect each other at right angles (90 degrees). This means they form a perfect “X” shape inside the kite. The formula for the area of a kite uses the lengths of these diagonals: Area = (Diagonal 1 × Diagonal 2) / 2.
3. Symmetry: The kite is symmetrical about the longer diagonal. This means that if you were to fold the kite along this diagonal, the two halves would match up perfectly. The longer diagonal acts like a mirror line, dividing the kite into two identical halves.
4. Bisected Diagonal: The longer diagonal bisects, or cuts in half, the shorter diagonal. This means that the longer diagonal divides the shorter diagonal into two equal parts at the point where they intersect.
5. Equal Opposite Angles: The angles opposite to the longer diagonal are equal. In other words, the two angles that are not next to each other and are on opposite sides of the longer diagonal are the same size.
6. Isosceles Triangles: The shorter diagonal splits the kite into two isosceles triangles. Isosceles triangles are triangles with two sides of equal length. In the case of the kite, these equal sides are the sides of the kite that form the shorter diagonal.

By understanding these properties, you can see how kites are a perfect blend of symmetry and balance. The equal sides, right-angle diagonals, and isosceles triangles all come together to make kites a fascinating topic in geometry!

Solving Math Problems Involving Kites

During your geometry classes, you will probably face a few mathematical problems that may involve kites. For this reason, we will include a few examples of such tasks and their detailed solutions so that you can use them as a guide in your future math classes.

Example 1: Finding the Area of a Kite

Problem:
Find the area of a kite with diagonals of lengths 10 cm and 6 cm.

Solution:

• Formula: The area of a kite is given by the formula: Area = (Diagonal 1 × Diagonal 2) / 2.
• Plug in the values: Substitute the lengths of the diagonals into the formula:
  • Area = (10 cm × 6 cm) / 2.
• Calculate: Multiply the lengths of the diagonals and then divide by 2:
  • Area = 60 cm² / 2 = 30 cm².
• Conclusion: The area of the kite is 30 cm².

Example 2: Finding the Measures of Angles in a Kite

Problem:
Find the area of a kite with diagonals of lengths 10 cm and 6 cm.

Solution:

1. Property: In a kite, one pair of opposite angles (the angles between the unequal sides) are equal.
2. Equal angles: Since one angle is 60°, the opposite angle is also 60°.
3. Supplementary angles: The other two angles in a kite are supplementary to the equal angles, meaning they add up to 180°.
4. Calculate the remaining angles: Each of the remaining angles is 180° – 60° = 120°.
5. Conclusion: The measures of the angles in the kite are 60°, 60°, 120°, and 120°.

Example 3: Calculating the Perimeter of a Kite

Problem:
Calculate the perimeter of a kite with sides of lengths 8 cm and 6 cm.

Solution:

1. Formula: The perimeter of a kite is the sum of all its sides. Since a kite has two pairs of equal sides, the formula can be simplified to:
   Perimeter = 2 × (Length of first pair of sides + Length of second pair of sides).
2. Plug in the values: Substitute the lengths of the sides into the formula:
   Perimeter = 2 × (8 cm + 6 cm).
3. Calculate: Add the lengths of the sides and then multiply by 2:
   Perimeter = 2 × 14 cm = 28 cm.
4. Conclusion: The perimeter of the kite is 28 cm.

Conclusion

While a kite shares some properties with parallelograms, it is not typically considered a parallelogram unless it is a rhombus. Understanding the unique properties of a kite, such as its diagonals and angles, can help in solving various geometrical problems and appreciating the diversity of shapes in geometry.

FAQ

Related

A*Help Insights - sign up for our Newsletter

Sign up

Thanks for signing up!

Something went wrong. Please try again later.

Follow us on Reddit for more insights and updates.