Understanding shapes and lines in geometry can be a daunting task for many. The distinction between various geometric figures, such as lines and line segments, often confuses students and enthusiasts alike. However, with the right guidance, this complex subject can be made accessible. This guide aims to ease readers into the intricate world of geometry, making the differentiation between lines and line segments clear and understandable.

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
Geometry surrounds us in every shape and form, with lines forming the essence of every two-dimensional plane we encounter. Lines, in their simplest form, are straight and extend infinitely in both directions without bends, thickness, or breadth, making them uni-dimensional. Identifying lines and understanding their role in forming geometric shapes is crucial. This knowledge becomes particularly important when differentiating between lines, line segments, and rays within these shapes.
What Is the Difference Between a Line and a Line Segment?
The primary distinction between a line and a line segment lies in their definitions and physical properties. A line extends infinitely in both directions and has no endpoints, embodying boundlessness. Conversely, a line segment is confined; it has two distinct endpoints and a finite length, making it a measurable part of a line.
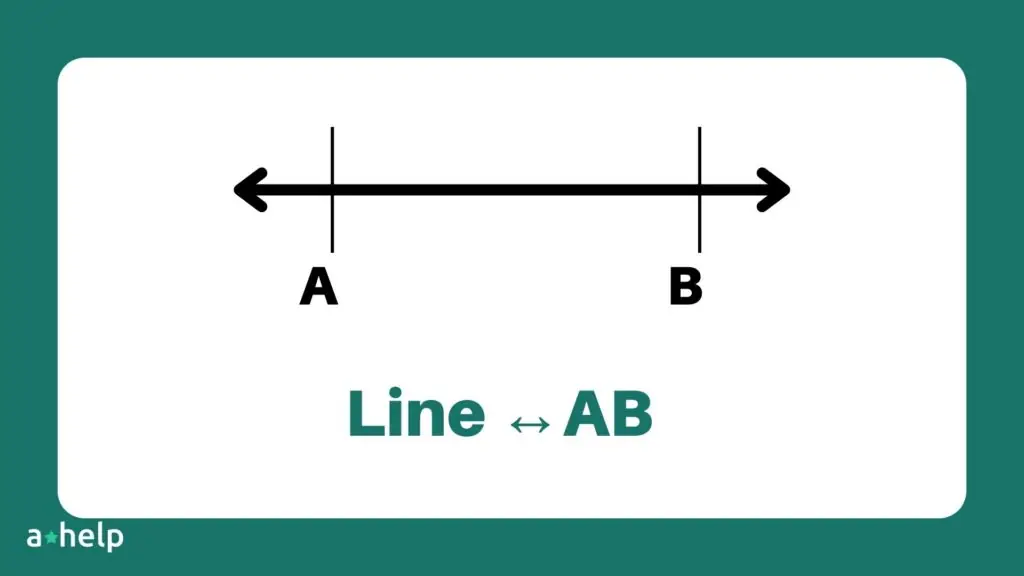
A line is a one-dimensional geometric figure that is straight, lacks thickness, and extends infinitely in both directions.
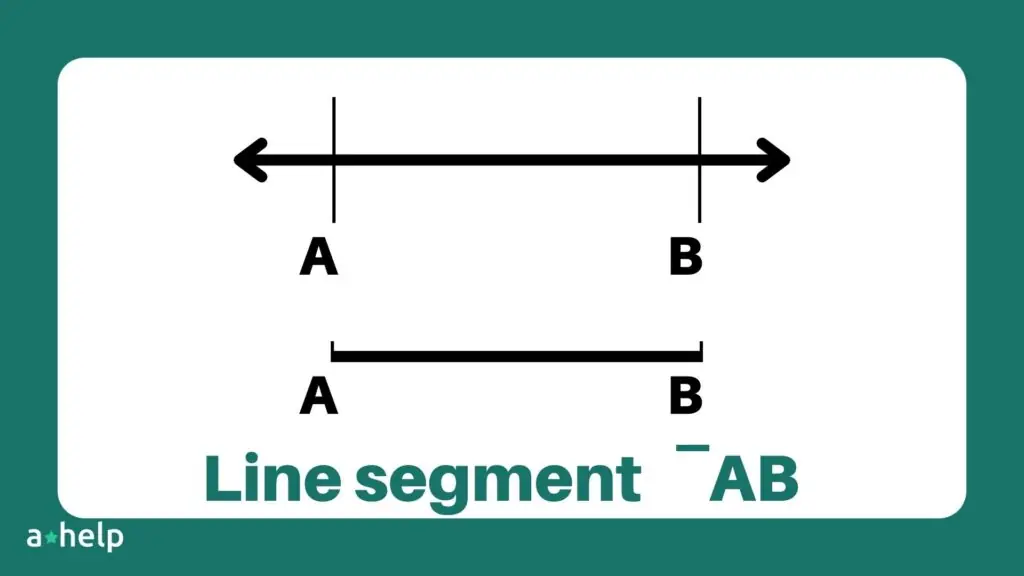
A line segment is the part of a line that lies between two distinct points, representing the shortest measurable distance connecting these points.
To better illustrate these differences, consider the following table that visually summarizes the main distinctions:
| Feature | Line | Line Segment |
|---|---|---|
| Endpoints | None; extends infinitely in both directions. | Two distinct endpoints. |
| Length | Indefinite; cannot be measured. | Definite; can be measured. |
| Representation | Denoted as ↔AB | Denoted as ‾AB |
| Nature | Boundless, continuous. | Finite, a specific part of a line. |
Understanding these differences is key to identifying and utilizing lines and line segments in geometric shapes effectively.
Facts about the Difference between Line Segment and Line
- 📏 Euclid’s Legacy: Euclid, often referred to as the Father of Geometry, was the first to introduce the concept of a line, which he described as “a breadthless length.” This foundational definition underscores the line’s infinite nature, contrasting with the measurable length of a line segment.
- ➡️ One Directional Ray: A ray, similar to a line, extends infinitely but only in one direction. It has a starting point, unlike a line, which resonates with the finite aspect of a line segment but differs due to its unbounded extension.
- 🔢 Collinear Points: A set of three or more points that align on the same straight line are termed collinear. This concept emphasizes the line’s ability to connect multiple points across its infinite span, a property not shared by the finite line segment.
- 📍 Unique Connection: Through any two given points, only one straight line can be drawn. This principle highlights the precise and defined nature of lines and line segments, underscoring their fundamental role in geometry.
- 📏 Dimensionality: Both lines and line segments are considered one-dimensional shapes. They possess length but lack width and depth, illustrating their simplicity and foundational importance in geometric principles.
Examples on Difference Between Line Segment and Line
In this article, we’ve explored the definitions and key differences between lines and line segments. To deepen our understanding, let’s work through some examples.
Task 1: Identifying Geometric Figures
Problem: Given different geometric figures: a line, a line segment, a ray, and a point, identify each one correctly.
Task 2: Naming Geometric Figures
Problem: Given two figures, one representing a line segment AB and another representing a line passing through points A and B, correctly name each figure.
Task 3: Finding Possible Line Segments
Problem: Given a figure with points A, B, C, and D aligned on a straight path, identify all possible line segments that can be formed by connecting these points.
Wrap Up
With the help of this guide, readers should find it easier to navigate the complexities of lines in geometry. By understanding the essential differences between lines and line segments, from their definitions to their representation and properties, one can appreciate their significance in the geometric landscape. This knowledge not only aids in academic pursuits but also enhances our understanding of the geometric principles that structure the world around us.
FAQ
Follow us on Reddit for more insights and updates.




Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.