In geometry, understanding opposite rays is foundational for grasping more complex concepts. This article explores what opposite rays are and how they play a crucial role in the world of shapes and lines.

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
Opposite rays might sound like a complex term, but they’re a basic concept in geometry that helps us understand angles and lines better. By breaking down this idea, we’ll see how opposite rays are not just theoretical but also practical in everyday geometry problems.
What Are Opposite Rays?
Opposite rays are two rays that share the same endpoint and extend infinitely in opposite directions. Imagine standing on a straight road that stretches as far as the eye can see in both directions. Here, you are the shared endpoint, and the endless roads are the rays extending in opposite directions. This concept is fundamental because it helps us understand how lines and angles are formed and interact with each other.
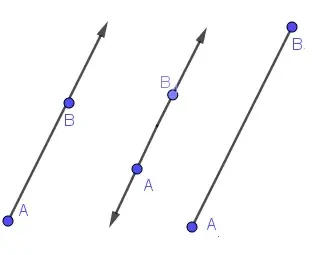
Key Characteristics of Opposite Rays:
- Shared Endpoint: The two rays have a common starting point but extend indefinitely away from each other.
- Infinite Length: Like all rays, opposite rays continue infinitely, illustrating the idea of endless distance in geometry.
- Straight Line Formation: When you put two opposite rays together, they form a straight line, highlighting the concept of linear geometry.
Examples in Everyday Geometry
- A Road: As mentioned, a straight road extending in two directions from a point where you stand.
- Light Beam: Imagine a flashlight shining in one direction, while its opposite direction can be thought of as an opposite ray if extended infinitely.
- Sunrise and Sunset Directions: At sunrise, the sun’s rays in the eastern horizon and its opposite in the western horizon at sunset can be visualized as opposite rays.

Importance of opposite rays in geometry
Opposite rays are not just a theoretical concept; they have practical implications in understanding and solving geometric problems. They are particularly useful in studying angles, constructing geometric figures, and solving problems related to parallel lines and angle bisectors.
| Concept | Description | Example |
|---|---|---|
| Role in Angle Formation | Two rays that originate from the same point and extend in opposite directions form a straight angle of 180 degrees. This principle is key to understanding angles and is used in proving geometric theorems. | Compass Directions: Imagine standing at a point where one ray points north and the other points directly south, forming a straight angle. |
| Application in Geometric Constructions | The concept of opposite rays is utilized in drawing straight lines, bisecting angles, and constructing parallel lines. It aids in creating precise geometric constructions by ensuring accurate angle measurements and divisions. | Angle Bisector: When bisecting an angle, the bisector divides the angle into two equal parts. If the original angle is a straight angle (180 degrees), the bisector creates two right angles (90 degrees each), with the opposite rays at the base of the original angle serving as guides for precision. |
Opposite rays are a simple yet profound concept in geometry that extend our understanding of lines, angles, and spatial relationships. By recognizing how two rays can share a starting point and stretch infinitely in opposite directions, we can better grasp the nature of geometric figures and solve complex problems with ease. Whether it’s through the visualization of a road or the beam of a flashlight, opposite rays are everywhere, illustrating the beauty and consistency of geometric principles in our everyday world.
FAQ
Follow us on Reddit for more insights and updates.




Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.