In the world of geometry, various elements and concepts play a significant role in understanding the structure of shapes and angles. One such fundamental concept is a ray. In this article, we will delve into the definition of a ray in geometry, explore relevant examples, and discuss its important properties. For readers seeking a more hands-on experience with these concepts, online tutoring sites offer interactive lessons.

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
Definition of a Ray
A ray is a fundamental geometric figure that consists of a part of a line with a fixed starting point, known as the endpoint, and extends infinitely in one direction. It can be visualized as an arrow pointing towards infinity. Rays are essential building blocks for constructing angles and understanding the relationship between lines and points.
Examples of Rays
To grasp the concept of a ray more effectively, let’s consider a few examples. Imagine the sun’s rays spreading across the sky at sunrise or sunset. The sun represents the starting point or endpoint of the ray, while the rays themselves extend infinitely into space.
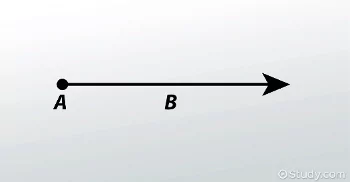
Naming a Ray
When it comes to identifying and naming a ray, we use the initial endpoint and any other point through which it passes. For instance, if we have a ray passing through points A and B, we can name it as ray AB or ray BA. The endpoint is the origin point from which the ray embarks on its endless journey.
Angles and Rays
Rays are closely associated with angles. When two rays share a common endpoint, they form an angle. The vertex of the angle is the starting point of the rays, while the arms of the angle are the rays themselves. By measuring the angle between the rays, we gain insights into the degrees of rotation between them.
Properties of Rays
Understanding the properties of rays is crucial in geometry. Here are a few key properties:
- Infiniteness: A ray extends infinitely in one direction, without an endpoint or termination point.
- Unidirectionality: A ray can only be traversed in one direction from the endpoint, towards infinity.
- No Length Measurement: Unlike line segments, rays do not have a measurable length since they extend infinitely.
Conclusion
Rays are fundamental geometric elements that provide a foundation for understanding angles, lines, and points in geometry. By comprehending the definition and properties of rays, we can effectively analyze and construct angles, enabling us to explore the intricate world of polygons and geometric figures.
Remember, rays are infinite and unidirectional, serving as essential tools for geometric exploration. Embrace the concept of rays, and unlock a deeper understanding of geometry’s intricacies.
FAQ
How do you identify rays in geometry?
To identify rays in geometry, look for lines that have a starting point and extend infinitely in one direction. Rays have an endpoint where they begin and continue indefinitely without reaching an endpoint in the opposite direction.
What is the relationship between a ray and an angle?
Rays and angles are closely related in geometry. When two rays share a common endpoint, they form an angle. The common endpoint of the rays is referred to as the vertex of the angle, while the rays themselves are known as the arms of the angle. The measurement of the angle is determined by the degree of rotation between the arms of the angle.
What is the difference between a ray and a line segment?
The key distinction between a ray and a line segment lies in their characteristics:
- Ray: A ray is a part of a line that has a fixed starting point (endpoint) but continues indefinitely in one direction. It does not have an endpoint on the other side and can be represented by an arrowhead. Rays extend infinitely.
- Line Segment: A line segment, on the other hand, is a portion of a line that has two distinct endpoints. It is a finite section of a line and has a measurable length. Unlike rays, line segments do not extend indefinitely in a particular direction.
Understanding these differences is crucial in geometry as they help in visualizing and analyzing geometric figures and their properties.
Follow us on Reddit for more insights and updates.




Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.