What is CPCTC in Geometry

CPCTC is an abbreviation of a theorem that stands for Corresponding Parts of Congruent Triangles are Congruent. It is used in geometry to conclude that if two triangles are congruent, then all their corresponding parts (angles and sides) are also congruent. In simpler terms, if two triangles are identical in shape and size, then each part of one triangle matches perfectly with the corresponding part of the other triangle.

The CPTC is an important concept in geometry. That’s why we wanted to dig a bit deeper into this concept and try to explain it to you quickly and simply.

The CPCTC Theorem Explained

Before trying to explain the theorem, let’s figure out what congruence is first. So, in geometry, two figures are considered congruent if they have the same shape and size. This means that every corresponding part of one figure matches perfectly with the corresponding part of the other figure. This explains why if we are given a condition that two triangles are congruent, it means their angles and sides are congruent (similar) too.

For example, if triangle ABC is congruent to triangle DEF, then side AB is equal in length to side DE, side BC is equal to side EF, side AC is equal to side DF, angle A is equal to angle D, angle B is equal to angle E, and angle C is equal to angle F.

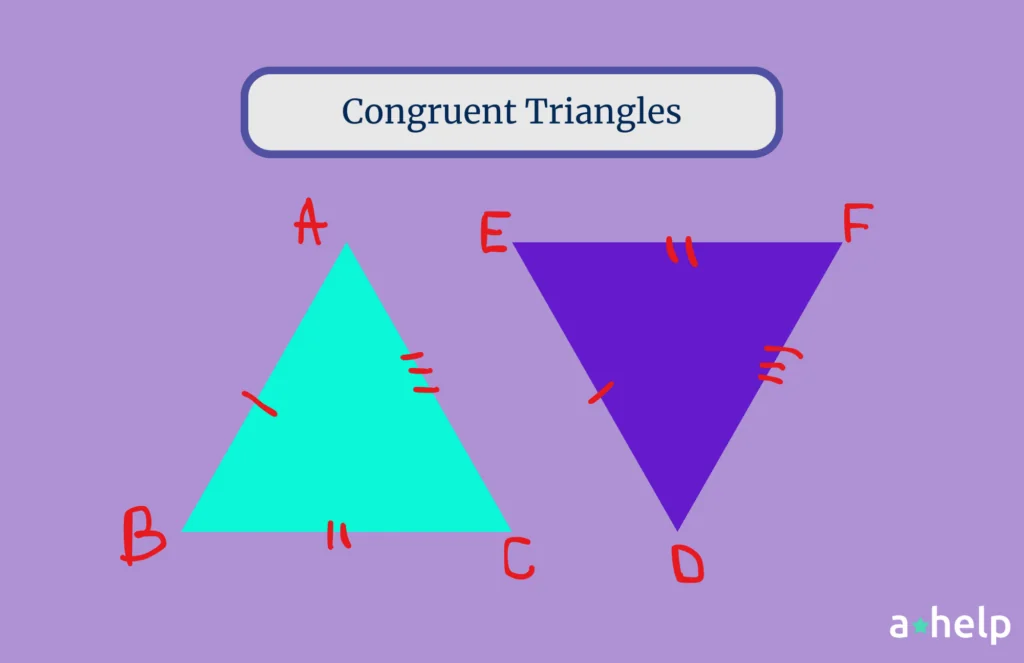
The CPCTCC Theorem therefore states, that if two triangles are congruent, then not only are their three sides and three angles equal, but also every corresponding part of the triangles is equal. This basically includes any segments or lines that are part of the triangles.

Oftentimes, this theorem is used in the final stages of geometrical proofs. After using one of the five congruence criteria (which we will discuss a bit further in the article) to prove that two triangles are congruent, we can then use CPCTC to state that all their corresponding parts are congruent. What is so useful about this theorem is that with its help you can then prove other properties as well, such as the congruence of other figures or the parallelism of lines.

The 5 Criteria of Triangle Congruence

So now, as we finally clarified what is congruence and what lies in the core of the CPCTC theorem, we can move on to the major question: how do we find whether the triangles are similar (read congruent) or not?

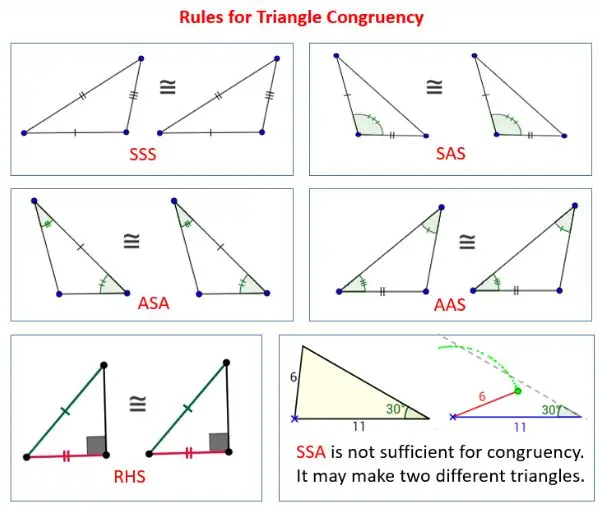
As shown on the image above, there are 5 tell-tale signs that can help pinpoint the two triangles that are exactly the same:

Criteria	Description
Side-Side-Side (SSS)	3 sides of one triangle = to 3 sides of another triangle => the triangles are congruent.
Side-Angle-Side (SAS)	2 sides and the included angle of one triangle = to 2 sides and the included angle of another triangle => the triangles are congruent.
Angle-Side-Angle (ASA)	2 angles and the included side of one triangle = to 2 angles and the included side of another triangle => the triangles are congruent.
Angle-Angle-Side (AAS)	2 angles and a non-included side of one triangle = to 2 angles and a non-included side of another triangle => the triangles are congruent.
Right Angle-Hypotenuse-Side (RHS)	If the hypotenuse and 1 leg of a right triangle = to the hypotenuse and 1 leg of another right triangle => the triangles are congruent.

Let’s also look into why each of the criteria works when proving congruence:

1. In SSS the side lengths are the ones to determine the shape and size of the triangle.
2. If we follow the SAS criteria, we will see that the included angle is crucial since it is what ensures that the overall shape of the triangles is the same.
3. Similar to SAS, in the ASA criterion, the included side is important for maintaining the shape of the triangles.
4. In the case of AAS though, unlike ASA, the side does not have to be between the angles, which provides more flexibility in proving congruence.
5. Finally, as to the Right Angle-Hypotenuse-Side-based criterion, the right angle is what ensures that the triangles have the same shape. The equal sides also ensure they are the same size.

Applying the CPCTC Theorem in Geometrical Problems

Why did we learn all of this? The obvious reason is to solve math problems during your geometry classes. And, as we previously mentioned, the CPCTC theorem is mostly used in geometrical proofs. However, it can also be appllied for constructions, where establishing the congruence of triangles is a major part of the building process. We decided to get into this topic a little bit deeper, and so we found a few instances, where the theorem would play a central role:

Proving Properties of Figures
CPCTC can be used to prove properties such as the parallelism of lines, the equality of angles, and the congruence of segments.

Constructing Geometric Shapes
In geometric constructions, this theorem helps ensure that the constructed shapes have the desired properties and dimensions.

Solving Problems Involving Triangles
Many problems in geometry involve finding unknown angles or sides of triangles. By proving triangles congruent and applying CPCTC, these unknowns can be easily and quickly determined.

By the way, aside from math, this theorem can also be applied in real-life situations. For example, when designing symmetrical structures, architects use the concept of congruent triangles to ensure that corresponding parts of the structure are equal and balanced. CPCTC helps in verifying that architectural elements like trusses, gables, and arches are congruent and properly aligned. It can also successfully be used to help in engineering (for proper engine building), art & design (for symmetry), as well as navigation and surveying (mostly to accurately determine distances between objects). As you see, the application of CPCTC theory is pretty vast, so think twice before giving up on trying to learn it. Who knows, maybe it will prove helpful to you in the end.

Doing Geometry: Examples of Geometrical Problems Using CPCTC

Problem 1
Prove that the base angles of an isosceles triangle are congruent.

Solution
Let ABC be an isosceles triangle (meaning it has 2 sides of equal length) with AB = AC.
By the Side-Side-Side (SSS) criterion, triangle ABC is congruent to triangle ACB.
By CPCTC, angle BAC is therefore congruent to angle BCA.

Problem 2
In triangle ABC and triangle DEF, AB = DE, BC = EF, and angle B = angle E.
Prove that triangle ABC is congruent to triangle DEF.

Solution
By the Side-Angle-Side (SAS) criterion, triangle ABC is congruent to triangle DEF.
Therefore, by CPCTC, AC = DF and angle C = angle F.

FAQ

Related

A*Help Insights - sign up for our Newsletter

Sign up

Thanks for signing up!

Something went wrong. Please try again later.

Follow us on Reddit for more insights and updates.