Center of Mass Formula: Explained

The concept of the center of mass (COM) is a foundational principle in physics and engineering. It is the point in a system or an object where the distribution of mass is equal in all directions. This position is crucial when analyzing the motion, stability, and gravitational interactions of an object.

JOIN OUR LEARNING HUB

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator

Get Free Tools

Defining Center of Mass

In physics, the center of mass of an object or system is a point that represents the average position of all the parts of the system, weighted according to their masses. For simple geometric objects with uniform density, the center of mass is the same as the geometric center. However, for irregular objects or systems of multiple objects, the center of mass location may not be intuitively obvious and requires calculation.

The Importance of COM in Physics

The center of mass plays a pivotal role in various physical phenomena:

Stability: The lower the center of mass, the more stable an object is. This is important in understanding why and how objects topple.
Motion: In a gravitational field, all parts of an object are pulled towards the center of the earth, but the motion of the object can be predicted by considering a force applied at the COM.
Rotation: Objects rotate about their center of mass. When calculating rotational dynamics, the point mass assumption simplifies an object to its center of mass.

The Center of Mass Formula

The formula for finding the center of mass for a system of point masses is given by:

where mi represents each mass in the system, and ri represents the position vector of each mass with respect to a chosen reference frame.

Application in Coordinate Systems

In a coordinate reference system, you can find the center of mass by calculating its coordinates (x, y, z) using the formula:

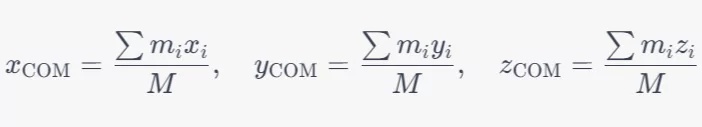
Here, xi, yi, and zi are the coordinates of each mass, and M is the total mass of the system.

Center of Mass in Various Contexts

In Mechanics

The center of mass is often used interchangeably with the center of gravity in a uniform gravitational field. This is the point where the force of gravity can be considered to act. In engineering mechanics, understanding the center of gravity is essential for designing stable structures and vehicles, as it relates to their topple limit. For example, knowing the center of mass location is critical in preventing trucks from toppling over when taking sharp turns.

In Elastic Collisions

During an elastic collision, the velocities of the colliding objects can be analyzed using the center of mass frame (COM frame). This frame of reference simplifies the calculation since the total momentum in the COM frame is zero, making the analysis of the collision more straightforward.

Irregular Objects

For irregular objects, the center of mass may not correspond with any actual material point within the object. For instance, the centroid of a donut-shaped object lies in its central void. Here, the plumb line method can be applied to experimentally determine the center of mass by suspending the object from different points until a common intersect is found.

Practical Considerations

Moving Frames

In a moving reference frame, the center of mass of a system can provide insights into its dynamics. In the case of a high-speed vehicle, for example, understanding the motion in the COM frame can help optimize stability and control.

Laboratory Analysis

In a laboratory setting, the center of mass is an essential concept for experiments involving balance and the analysis of forces. It helps in setting up the coordinate reference systems and ensuring the accuracy of measurements.

Conclusion

The center of mass formula is a powerful tool in physics and engineering. Whether dealing with the stability of structures, the dynamics of motion, or the precision of laboratory experiments, the ability to calculate the COM provides essential insights into the behavior of physical systems. By applying this fundamental principle, we can predict how an object will react under various forces and motions, making it a cornerstone of scientific and engineering analysis.

FAQ

Why is the center of mass important in physics?

The center of mass is a critical concept in physics because it simplifies the analysis of motion. Instead of dealing with the motions of potentially millions of individual particles in an object, physicists can treat the entire mass as if it were concentrated at the center of mass. This makes it easier to predict the effects of forces and the behavior of objects when interacting with their environment. In areas such as mechanics, astronomy, and engineering, the center of mass is vital for understanding balance, stability, and motion.

Can you explain the concept of center of mass in simple terms?

The center of mass is like the balancing point of an object or group of objects. It’s the point where you could balance the object on the tip of your finger if all the weight was concentrated there. If you have different objects or parts of an object with different weights, the center of mass takes all these into account and tells you exactly where that balancing point is. Imagine holding a ruler with a heavy eraser on one end; the center of mass will be closer to the eraser because there is more weight on that side.

Are there different formulas for calculating the center of mass?

Yes, there are different formulas for calculating the center of mass depending on the complexity of the object or system. For a simple two-object system, the formula is a weighted average of their individual positions. For continuous objects, the calculation integrates over the entire volume of the object, taking into account the density distribution. For symmetrical objects, the center of mass can often be inferred based on symmetry alone. The specific formula used is chosen based on the nature of the objects and their mass distribution.

What are some practical applications of the center of mass formula?

The center of mass formula has many practical applications. In vehicle design, it helps ensure stability and safety. In sports, athletes use the concept to improve their performance, like a diver spinning around their center of mass to achieve graceful flips. In construction, it’s used to build stable structures that can withstand various forces. In space, it helps in understanding the motion of celestial bodies and in the design of stable spacecraft. Essentially, any situation that involves balance, motion, or stability can benefit from understanding and applying the center of mass formula.

Are there any common misconceptions about the center of mass formula?

One common misconception is that the center of mass must always be located within the physical bounds of an object, which is not true. For example, the center of mass for a ring or a hollow sphere is actually in the empty space at the center of these objects. Another misconception is that the center of mass is fixed; it can change position if the shape of the object or the mass distribution changes. Additionally, the center of mass is often incorrectly thought to be the same as the center of gravity, which is only true when the gravitational field is uniform.

PHYSICS

Opt out or Contact us anytime. See our Privacy Notice

Comments (0)

Welcome to A*Help comments!

We’re all about debate and discussion at A*Help.

We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.

Understanding the Center of Mass Formula