What Is a Quantum Mechanical Model?

In the vast realm of physics, the quantum mechanical model stands as one of the cornerstones of our understanding of the microscopic world. This model, often associated with mind-bending concepts and peculiar behaviors, delves into the fundamental nature of particles, electrons in particular, and their enigmatic properties. In this guide, we will unravel the mysteries of the quantum mechanical model, exploring its key components, implications, and significance in the realm of modern physics.

 

The Quantum Mechanical Model Unveiled

At its core, the quantum mechanical model presents a novel way of perceiving the behavior of particles, transcending classical physics and introducing us to a world governed by probability and wave functions. Let’s delve into its key components.

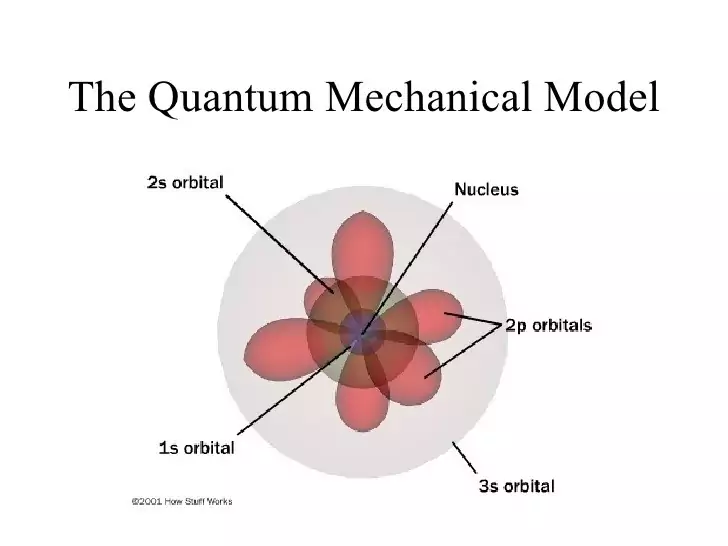
Quantum Mechanical Model Components

Quantum Numbers: The quantum mechanical model introduces the concept of quantum numbers, which play a pivotal role in characterizing the behavior of particles within atoms. These numbers, often referred to as the roadmap of electrons, include the principal quantum number (n), azimuthal quantum number (l), magnetic quantum number (ml), and spin quantum number (ms). Quantum numbers are fundamental in understanding electron configurations within an atom.

Erwin Schrödinger proposed the Schrödinger equation, a fundamental equation in quantum mechanics. This equation is the cornerstone of the quantum mechanical model, providing a mathematical framework for describing the behavior of matter waves, including electrons. The Schrödinger equation yields a series of wave functions that are associated with different energy levels and characterize the probability of finding an electron in a given region within the atom.

Atomic orbitals are the regions within an atom where electrons are likely to be found about 90% of the time. These regions are defined by the square of the wave function (ψ²), which represents the probability density. The concept of atomic orbitals is crucial in understanding the spatial distribution of electrons within atoms.

The Heisenberg Uncertainty Principle

One of the most intriguing aspects of the quantum mechanical model is the Heisenberg uncertainty principle. This principle states that it is impossible to simultaneously know both the energy and position of an electron with absolute certainty. As we strive to pinpoint an electron’s position more accurately, we become less certain about its energy, and vice versa. This inherent uncertainty challenges our classical intuition but is a fundamental aspect of quantum mechanics.

Matter Waves and Wave-Particle Duality

Wave-Particle Duality

French physicist Louis de Broglie made a groundbreaking contribution to quantum mechanics by proposing the concept of wave-particle duality. This notion suggests that particles, such as electrons, can exhibit both particle-like and wave-like properties. De Broglie’s equation for the wavelength of a particle is:

Notably, the wavelength of a particle is inversely proportional to its mass, implying that the wave-like behavior becomes significant for particles with very small masses, such as electrons.

Standing Waves

The quantum mechanical model draws inspiration from standing waves, a concept familiar to those acquainted with stringed musical instruments. In a standing wave, there are points of zero displacement known as nodes. These nodes limit the allowable wavelengths for any standing wave, leading to the quantization of energy levels, a fundamental aspect of the quantum mechanical model.

Atomic Orbitals and Probability Density

Shapes of Atomic Orbitals

While spherical s orbitals are a straightforward concept in atomic orbitals, other types such as p, d, and f orbitals introduce intriguing spatial variations. For instance, p orbitals are shaped like dumbbells oriented along specific axes, while d orbitals can be described as clover-shaped with multiple orientations. These orbital shapes are determined by the probability distribution of electrons within atoms.

Probability Density Visualization

The probability density represents the likelihood of finding an electron in a particular volume of space within an atom. Visualization of probability density can take various forms, such as graphical representations that use color intensity to denote relative probabilities. Regions with higher probabilities exhibit denser colors, aiding in understanding electron distribution within atomic orbitals.

Electron Spin and the Stern-Gerlach Experiment

Electron Spin

Electron spin is an intrinsic property that sets electrons apart in the quantum mechanical model. It introduces the concept of spin-up and spin-down, signifying two possible spin values for electrons. This property has profound implications, including the Pauli exclusion principle, which states that no two electrons in the same orbital can have the same spin.

Stern-Gerlach Experiment

German physicists Otto Stern and Walther Gerlach conducted the Stern-Gerlach experiment to explore electron spin. This experiment revealed that electrons could only exhibit two possible orientations when subjected to a magnetic field: aligning with the magnetic field or opposing it. The results of this experiment defied classical physics and underscored the quantum nature of electrons.

Conclusion

The quantum mechanical model, with its quantum numbers, Schrödinger equation, atomic orbitals, and the Heisenberg uncertainty principle, provides a profound framework for understanding the behavior of particles at the microscopic level. Wave-particle duality challenges our classical notions, while the concept of atomic orbitals and probability density offers insights into electron distribution within atoms. Electron spin and the Stern-Gerlach experiment further highlight the mysterious yet captivating world of quantum mechanics. Embracing the quantum mechanical model is essential for unraveling the intricacies of the quantum realm and advancing our understanding of the fundamental building blocks of the universe.

FAQ

A*Help Insights - sign up for our Newsletter

Sign up

Thanks for signing up!

Something went wrong. Please try again later.

Follow us on Reddit for more insights and updates.