Flux in physics quantifies the flow of electric or magnetic fields through a surface, vital for understanding electromagnetic phenomena and their practical applications in various fields.

✅ AI Essay Writer ✅ AI Detector ✅ Plagchecker ✅ Paraphraser
✅ Summarizer ✅ Citation Generator
In the realm of physics, flux is a fundamental concept that measures how much of an electric or magnetic field passes through a given surface. This concept is not only pivotal in comprehending electromagnetic fields but also extends its utility to various sectors, including technology and entertainment. The visualization of field lines, or lines of force, plays a crucial role in understanding flux, offering insights into the field’s strength and direction. This article aims to demystify the concept of flux, providing a comprehensive yet accessible exploration of its principles, applications, and significance.
What is Flux?
Flux in physics relates directly to the concept of field lines, an essential tool for visualizing electric and magnetic fields.
These imaginary lines illustrate the direction and magnitude of a field, greatly aiding in the measurement and understanding of flux. The density of these lines indicates the strength of the field: the denser the lines, the stronger the field. For example, if more lines pass through a surface area, it indicates a higher flux due to a stronger field. This direct proportionality between field lines and flux is crucial in understanding how fields interact with materials and surfaces.
Several factors influence the rate of flux through a surface.
First and foremost, the strength of the field plays a significant role. An increase in field strength directly increases the flux. For instance, doubling the strength of a field doubles the flux.
Secondly, the surface area through which the field lines pass is equally important. A larger area can accommodate more field lines, resulting in a higher flux.
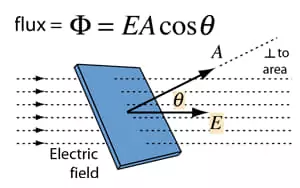
Lastly, the angle at which field lines intersect with a surface critically affects the flux. Field lines perpendicular to the surface contribute to the highest rate of flux. As the angle deviates from this perpendicular orientation, the effective area through which field lines can pass decreases, leading to a reduction in flux.
Practical Implications and Calculations
Flux is not just a theoretical concept but has a precise mathematical formulation. For electric flux, the equation is ΦE = EA cos θ, where Φ represents flux, E is the electric field’s magnitude, A is the surface area, and θ is the angle between the field lines and a perpendicular line to the surface (the normal vector). This formula elegantly encapsulates the relationship between field strength, surface area, and the angle of intersection. A similar formula applies to magnetic flux, substituting the electric field magnitude with that of the magnetic field.
Flux in Various Fields and Everyday Life
Beyond its theoretical importance in physics, the concept of flux finds applications in numerous other domains. In medicine, it describes the flow of fluids in or out of the body. In fluid dynamics, it refers to water flow in streams. In metalwork, flux is a substance aiding in the bonding of metals. In computing, it appears in AI development and cybersecurity. Moreover, flux has even made its way into popular culture, with references like the ‘flux capacitor’ in the “Back to the Future” films. This wide-ranging applicability underscores the versatility and significance of understanding flux in physics.
Flux is a fundamental concept in physics that provides a window into the behavior of electric and magnetic fields. By understanding how field lines interact with surfaces, we gain crucial insights into the nature of electromagnetic phenomena. The concept’s mathematical formulation allows for precise calculations and predictions, further enhancing its utility in various scientific and technological fields. Whether in theoretical physics or practical applications, the concept of flux remains an essential tool for understanding and harnessing the power of electromagnetic fields.
FAQ
Follow us on Reddit for more insights and updates.





Comments (0)
Welcome to A*Help comments!
We’re all about debate and discussion at A*Help.
We value the diverse opinions of users, so you may find points of view that you don’t agree with. And that’s cool. However, there are certain things we’re not OK with: attempts to manipulate our data in any way, for example, or the posting of discriminative, offensive, hateful, or disparaging material.